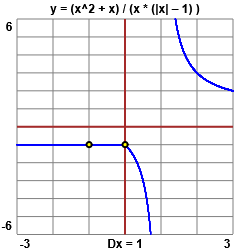
plot (x^2 + x) / (x * (|x| - 1) ), -3 < x < 3
Schizza il grafico della seguente funzione, e controllalo, poi, al computer mediante una opportuna applicazione.
Stabilisci se è possibile estendere la funzione ad un dominio più ampio in modo che in esso sia continua.
x → (x2 + x) / (x · (|x| – 1) )
Ci conviene prima operare qualche manipolazione algebrica:
(x2 + x) / (x · (|x| – 1) )
equivale a
(x · (x + 1) ) / (x · (|x| – 1) ) che:
se x > 0 equivale a (x+1)/(x–1),
se x < 0 equivale a (x+1)/(–x–1) = –1, a patto che x≠-1, in cui la funzione non è definita,
se x = 0 è indefinito.
•
A sinistra dell'asse y il grafico coincide (per x≠-1) con la retta y = –1, e quindi:
limx → –1+F(x) = limx → –1–F(x) = –1.
• A destra dell'asse y il grafico coincide con y = (x+1)/(x–1), ossia y = 1+2/(x–1) (iperbole con asintoti x=1 e y=1)
[ci si può arrivare facendo la divisione: 1 con resto 2, o con: (x+1)/(x–1) = ((x–1)+1+1)/(x–1) = 1+2/(x–1)]
•
Per x = 0 sia la retta che l'iperbole hanno y = –1.
Quindi lì il grafico della nostra funzione (chiamiamola F) tende a congiungersi, senza arrivare a farlo in quanto ivi la funzione non è definita:
limx → 0+F(x) = limx → 0–F(x) = –1.
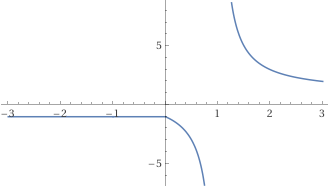
| Ecco, a destra il grafico ottenuto con questo script. Ha due "buchi", in |  |
| Il grafico è ottenibile facilmente anche con WolframAlpha: plot (x^2 + x) / (x * (|x| - 1) ), -3 < x < 3  |
Se definisco
G(x) = –1 se x=0 o x=-1, G(x) = F(x) =(x2 + x) / (x · (|x| – 1) ) altrimenti,
ottengo una funzione G che nel suo dominio (l'insieme dei numeri reali diversi da 1)
è continua e coincide con la funzione F iniziale nel dominio di essa.
Non è possibile estenderci a tutto l'intervallo dei numeri reali in quanto per x = 1 l'iperbole ha un asintoto.
Per altri commenti:  limiti neGli Oggetti Matematici.
limiti neGli Oggetti Matematici.