La funzione F: x → (2^x – 1) / x non è definita per x=0. È possibile definire una funzione G continua in tutto R che coincide con F per tutti gli altri input (la cosa può essere dimostrata; qui limitiamoci a prenderla per buona). Si approssimi il valore di G(0) a 6 cifre. Si affronti il problema usando opportunamente una calcolatrice tascabile.

Tracciando il grafico di F "a mano" o con l'aiuto del computer intuisco che F sia per x → 0+ che per x → 0- tende a un certo numero, vicino a 0.7, che potrò assumere come G(0). Non ci preocupiamo di una dimostrazione rigorosa di questo fatto, in quanto il testo dell'esercizio ci dice di prendere per buono il fatto che si possa definire G che abbia questa proprietà

Con una calcolatrice vediamo quanto vale F(x), ossia (2^x – 1) / x per valori di x man mano più vicini a 0. Utilizziamo online "calcolatrice2" presente qui ottenendo:

( pow(2,1e-1)-1 ) / 1e-1 = 0.7177346253629313
( pow(2,1e-2)-1 ) / 1e-2 = 0.6955550056718884
( pow(2,1e-3)-1 ) / 1e-3 = 0.6933874625807412
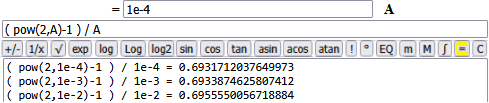
( pow(2,1e-4)-1 ) / 1e-4 = 0.6931712037649973
( pow(2,1e-5)-1 ) / 1e-5 = 0.6931495828199629
( pow(2,1e-6)-1 ) / 1e-6 = 0.6931474207938493
( pow(2,1e-7)-1 ) / 1e-7 = 0.6931472040783149
( pow(2,1e-8)-1 ) / 1e-8 = 0.6931471840943004
( pow(2,1e-9)-1 ) / 1e-9 = 0.6931470952764585
(pow(2,1e-10)-1) / 1e-10 = 0.6931477614102732
(pow(2,1e-11)-1) / 1e-11 = 0.6931566431944702
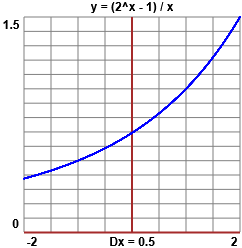
Si può anche notare che ad ogni divisione di x per 10, ossia man mano che si divide per 10 la distanza dal valore a chi facciamo tendere x, la variazione tra un output e il successivo è man mano più piccola, ossia i valori tendono a stabilizzarsi (si può osservare che al primo passo la variazione è 0.02, poi 0.002, poi 0.0002, …). Osserviamo che ciò accade fino a 1e-8; dopo, questa regolarità svanisce a causa degli errori di arrotondamento dovuti al fatto che il computer opera con un numero limitato di cifre. Posso assumere 0.69314718 come arrotondamento del limite per x che tende a 0+ di F e quindi come valore di G(0). Se non avessimo saputo che la funzione era "prolungabile" in 0 in modo da essere continua, avremmo dovuto studiare il limite anche per x che tende a 0-. Avremmo ottenuto una stabilizzazione sullo stesso valore.

Come arrotondamento a 6 cifre posso prendere tranquillamente 0.693147.

Con considerazioni teoriche meno elementari, una volta introdotta la funzione "logarimo naturale" (ln o log), si può stabilire che il valore esatto del limite è log(2) (= 0.693147180559945309417…), valore che posso ottenere con la calcolatrice vista sopra.

Per altri commenti: limiti neGli Oggetti Matematici.