F1, F2 e F5 sono definite ovunque, ossia in (-∞, ∞). Quindi dovremo studiarne il comportamento quando l'input tende a ∞ e a -∞. Il termine F3(x) (che contiene divisioni per x e per x³) non è definito per x=0, quindi dovremo studiarlo anche quando x → 0- e quando x → 0+. Analogamente dovremo studiare F4(x) (che contiene divisioni per x-4) anche quando x → 4- e quando x → 4+. Consideriamo le funzioni una per una.
F1)  2^x cresce al crescere di x.
Questo è evidente per gli x interi: le potenze di 2 sono tutti numeri positivi e per passare, ad es., da 2³ a 2⁴ moltiplico per 2 e, quindi, ottengo un numero più grande; in generale: 2ⁿ⁺¹ = 2ⁿ·2 > 2ⁿ. Ancora più in generale, se h è 0.1 o 0.01 o 0.001 o …, 2^x+h = 2^x·2^h > 2^x in quanto 2^0.1 = 2^1/10 = "numero che elevato alla 10 fa 2" > 1 (se fosse più piccolo di 1 mopltiplicandolo ripetutamente per esso stesso si otterrebbe un numero che rimarrebbe più piccolo di 1), 2^0.01 = 2^1/100 = … > 1, ecc. Comunque si apportino aumenti a x 2^x cresce.
Inoltre posso trovare x tale che 2^x sia grande quanto voglio: se ad es. prendo 10⁹, dato che 2⁴ = 16 > 10, ho che 2³⁶ = (2⁴)⁹ > 10⁹. Quindi 2^x → ∞ per x → ∞.
Per come abbiamo definito le potenze, 2^x > 0. E posso trovarne un valore vicino a 0 quanto voglio: se ad es. prendo 10^-9 ho che 2^-36 = (2⁴)^-9 < 10^-9 in quanto 1/16⁹ < 1/10⁹. Quindi 2^x → 0 per x → -∞.
Il grafico di x → 2^x ha quindi un andamento come quello rappresentato sotto a sinistra.

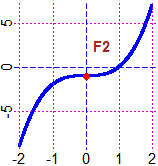
F2)  x³ cresce al crescere di x e non ha limitazioni superiori (per ogni input x maggiore di 1 l'output x³ è ad esso superiore); quindi x³→ ∞ per x → ∞. La parte di grafico a sinistra dell'asse y può essere ottenuta dall'altra parte per simmetria rispetto (ovvero mediante una rotazione di 180° attorno) all'origine; quindi x³→ -∞ per x → -∞.  x → x³–1 ha grafico traslato in basso di 1 e uguali comportamenti agli estremi del dominio.

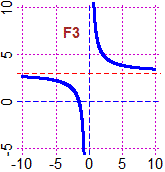
F3)  x → 4/x rappresenta una relazione di proporzionalità inversa; il suo grafico è un'iperbole; tende a 0 per x → ∞ e per x → -∞, tende a ∞ per x → 0+, tende a -∞ per x → 0-. x → 1/x³ ha un andamento simile. La funzione somma di esse avrà quindi un andamento analogo, e x → 3 + 4/x + 1/x³ rispetto a questa avrà grafico traslato verso l'alto di 3: vedi figura.

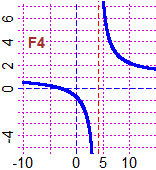
F4)  (3+x)/(x-4) non è definito per x=4, quindi dobbiamo studiare il suo comportamento per x → 4+ e x → 4- oltre che per x → ∞ e x → -∞. Potremmo ragionare direttamente su questo termine, ma è utile manipolarlo, in uno dei due seguenti modi:
• Eseguire la divisione tra i due polinomi x+3 e x-4: il quoziente è 1 e il resto è 7, per cui (3+x)/(x-4) equivale a 1+7/(x-4): il grafico è l'iperbole y=7/x traslata a destra di 4 e in alto di 1. F4(x) tende quindi a 1 per x → ∞ e x → -∞, a ∞ e a -∞ per x che tende a 4 rispettivamente da destra e da sinistra.
• Dividere i fattori del rapporto per x, in modo da trasformare il termine (x+3)/(x-4) in (1+3/x)/(1-4/x) (tenendo presente che è equivalente al precedente solo per x≠0 e x≠4, dove sono entrambi definiti). Questa forma consente di osservare facilmente che per x → ∞ e x → -∞ 3/x e 4/x tendono a 0 e quindi (1+3/x)/(1-4/x) tende a 1/1, ossia a 1. Per studiare il comportamento per x → 4+ e x → 4- questa trasformazione non ci è di aiuto: occorre ragionare sul termine di partenza o indifferentemente sul trasformato, osservare che avvicinandosi a 4 il primo termine del rapporto tende ad assumere un valore maggiore di 0 e che il secondo termine tende a 0 restando positivo o negativo a seconda che si arrivi a 4 da destra o da sinistra, concludendo che nel primo caso il limite è ∞ e nel secondo è -∞.

F5)  x →2^–x ha grafico simmetrico rispetto all'asse y a quello di x →2^x in quanto le due funzioni danno lo stesso output se si danno ad esse input opposti. Quindi, per quanto visto a proposito di F1, 2^–x → 0 per x → ∞, 2^–x → ∞ per x → -∞.

La rappresentazione grafica in JavaScript →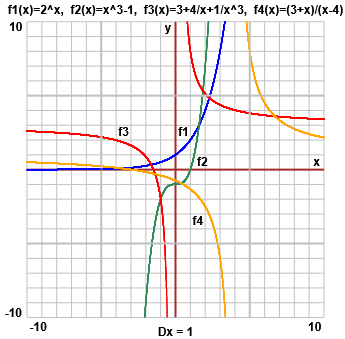

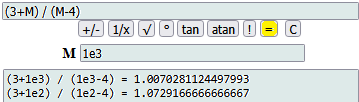← I limiti potrebbero essere studiati anche con lo script "calcolatrice" accessibile da qui.  A sinistra lo studio di  (3+x)/(x-4) per x → ∞. Mettendo in M   1e2, 1e3, ..., 1e15, 1e16, 1e17   ottengo   1.0729166666666667, 1.0070281124497993, ..., 1.000000000000007, 1.0000000000000009, 1

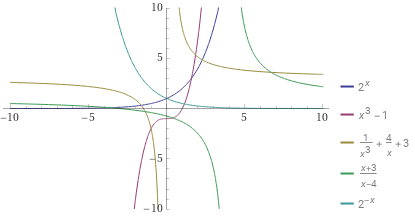
I grafici precedenti realizzati con WolframAlpha mediante il comando
plot y=2^x, y=x^3-1, y=3+4/x+1/x^3, y=(3+x)/(x-4), y=2^-x, -10<x<10, -10<y<10

Per altri commenti: limiti, strutture numeriche (per il significato di 2^x), funzione(2) e trasf. geometriche (per traslazioni e simmetrie di grafici), funz. polinomiali (per la divis. tra polinomi) neGli Oggetti Matematici.