Batti sulla calcolatrice un qualunque numero positivo e premi ripetutamente il tasto [√x] (in qualche modello occorre premere [inv] [x²], ossia selezionare la radice quadrata come "inversa" dell'elevamento al quadrato; in altri, in cui si possono scrivere sul visore più numeri ed operazioni, occorre prima premere [√x] e poi introdurre il numero). Oppure realizza un programma che dato un numero in input applichi a questo la radice quadrata, poi la riapplichi all'output, poi al nuovo output, e così via, stampando man mano gli output ottenuti.
Che cosa osservi? Sai esprimere il fenomeno osservato usando opportunamente il simbolo "lim"?
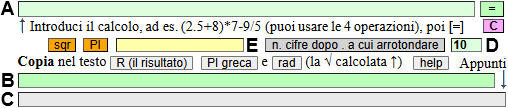
Per esemplificare, usiamo la "piccolissima" calcolatrice online presente QUI:
Se metto ad es. 2 nel box E e clicco ripetutamente [sqr] ottengo: 1.4142135624, 1.189207115, 1.0905077327, ..., 1.000000661, ..., 1.0000000007, 1.0000000004, 1.0000000002, 1
Se metto 0.3 ottengo: 0.5477225575, 0.7400828045, 0.8602806545, ..., 0.999999982, ..., 0.9999999998, 0.9999999999, 1
Esiti simili si ottengono con qualsiasi altro numero positivo (in qualche caso, con qualche calcolatrice, per problemi di arrotondamento, ci si può fermare su 0.999…9 o su 1.000…1).
Se indichiamo con x(.) la successione dei valori man mano visualizzati, ossia la successione: x(0) = "numero battuto inizialmente", x(1) = "numero ottenuto premendo [sqr] 1 volta, x(2) = "numero ottenuto premendo [sqr] 2 volte, … possiamo descrivere il fenomeno con:
|
Una descrizione più formale della successione può essere la seguente, dove k è il numero battuto inizialmente:
Un programma in JavaScript (vedi):
x=2; n=18
for(i=0; i<n; i=i+1) x=Math.sqrt(x); document.write(n*1," ",x,"<br>")
for(i=0; i<n; i=i+1) x=Math.sqrt(x); document.write(n*2," ",x,"<br>")
for(i=0; i<n; i=i+1) x=Math.sqrt(x); document.write(n*3," ",x,"<br>")
Uscite:
18 1.0000026441501502
36 1.0000000000100866
54 1
Per altri commenti: 
successioni e limiti neGli Oggetti Matematici.
Col software online WolframAlpha:
x(1) = 1/7, x(n+1) = sqrt(x(n))
x(1) = 2, x(n+1) = sqrt(x(n))
