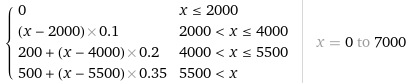| Nel paese Landia, la cui moneta è il Soldo (simbolo S), le imposte sono così stabilite: |
| reddito annuo | imposta |
| fino a 2000 S | 0 S |
| da 2000 S a 4000 S | 10% della parte di reddito eccedente 2000 S |
| oltre 4000 S | le imposte di chi ha 4000 S di reddito più il
20% della parte di reddito eccedente 4000 S | |
|
Sia F questa funzione reddito → imposta. Trascurando i problemi di arrotondamento (nella pratica, redditi e imposte non sono calcolati esattamente,
ma arrotondoti, ad esempio al Soldo o ai centesimi di Soldo o …), F è una funzione continua nel suo dominio [0,∞):
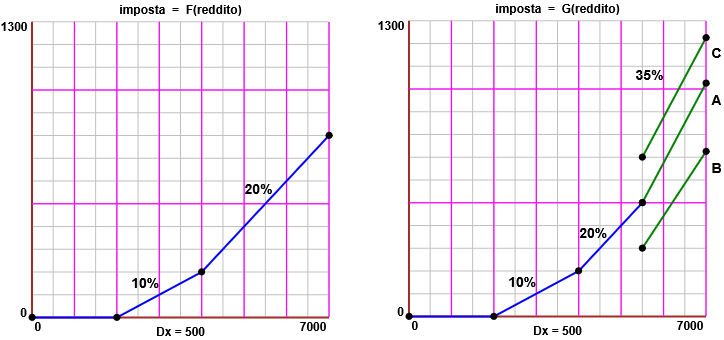
al variare del reddito l'imposta varia con continuità. Se voglio considerare uno scaglione di reddito in più, in modo che oltre 5500 S di reddito
l'aumento d'imposta sia pari al 35% dell'aumento di reddito, come si può definire la funzione G: reddito → imposta così da risultare
continua (ossia, vedi figura a destra, proseguire come A, non come B o C)? |
|
| |
| reddito | imposta = G(reddito) |
| fino a 2000 | 0 |
| da 2000 a 4000 | 10%(reddito – 2000) |
| da 4000 a 5500 | G(4000) + 20%(reddito – 4000) |
| oltre 5500 | G(5500) + 35%(reddito – 5500) | |
| ovvero, indicando con x il reddito in Soldi: |
| se x∈[0,2000] | G(x) = 0 |
| se x∈(2000,4000] | G(x) = (x – 2000)·0.1 |
| se x∈(4000,5500] | G(x) = 200 + (x – 4000)·0.2 |
| se x∈(5500,∞) | G(x) = 500 + (x – 5500)·0.35 | |
Per altri commenti:  proporzionalità, continuità neGli Oggetti Matematici proporzionalità, continuità neGli Oggetti Matematici |
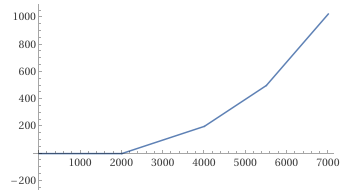
I grafici precenti sono stati realizzati con questo e questo script.
Altrimenti si può usare online www.wolframalpha.com. Vedi qui
plot piecewise[{ {0, x <= 2000}, {(x-2000)*0.1 , 2000 < x <= 4000}, { 200+(x-4000)*0.2 , 4000 < x <=5500}, { 500+(x-5500)*0.35 , 5500 < x} }], x = 0..7000
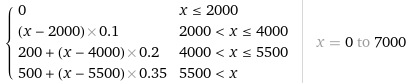


 proporzionalità, continuità neGli Oggetti Matematici
proporzionalità, continuità neGli Oggetti Matematici