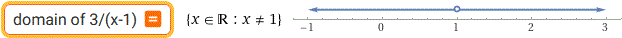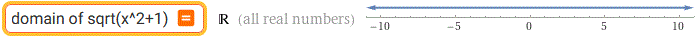Determinare il dominio delle funzioni:
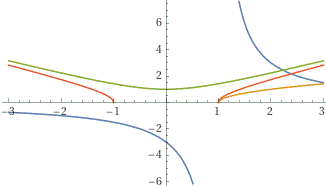
    F: x → 3/(x-1)       G: x → √(x-1)
    H: x → √(x²+1)       K: x → √(x²-1)

F)  l'insieme dei numeri x tali che x-1 ≠ 0, ossia l'insieme dei numeri diversi da 1
G)  l'insieme dei numeri x tali che 0 ≤ x-1, ossia tali che 1 ≤ x, ossia l'intervallo [1, ∞)
H)  l'insieme dei numeri x tali che 0 ≤ x²+1; questa relazione è sempre vera in quanto 0 ≤ x²; quindi il dominio è tutto R
K)  l'insieme dei numeri x tali che 0 ≤ x²-1, ossia tali che 1 ≤ x²; questa relazione è vera se 1 ≤ x o se x ≤ -1; il dominio è quindi costituito dagli intervalli (-∞, -1] e [1, ∞).

Per altri commenti: funzione (1) neGli Oggetti Matematici.

La rappresentazione grafica delle funzioni → (vedi QUI lo script con cui sono realizzati i grafici)

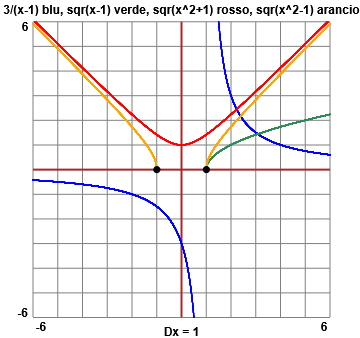Col software online WolframAlpha
plot 3/(x-1), sqrt(x-1), sqrt(x^2+1), sqrt(x^2-1), x = -3..3