|
È stato preso un cilindro graduato trasparente ed è stato posto sotto a un rubinetto facendo in modo che scenda un filo d'acqua.
Si rileva ogni 5 secondi il volume, in centilitri, raggiunto dall'acqua. Si ottengono i valori (approssimati) riportati sotto e rappresentati graficamente qui a destra. Qual è, approssimativamente, la funzione che al tempo trascorso associa il volume dell'acqua via via uscita. tempo (s) 0 5 10 15 20 25 30 35 40 volume (cl) 0 8 16 23 31 39 47 54 62 |  |
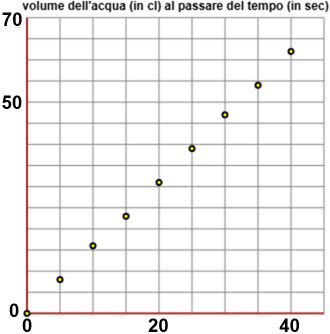
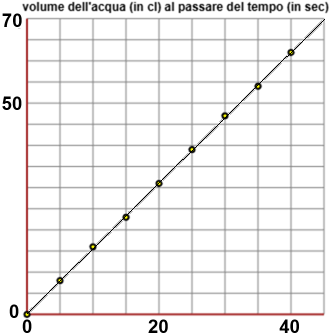
 | Si capisce che il volume di acqua che scende aumenta con velocità costante: i pallini sul grafico appaiono quasi perfettamente allineati, lungo una retta passante per il punto (0,0). Cerchiamo di individuare questa retta come grafico di una opportuna funzione. Troviamone la pendenza. La retta tracciata a sinistra passa quasi perfettamente per l'ultimo punto, che a 40 (secondi) associa 62 (centilitri). Se indichiamo con x i secondi e con y i centilitri possiamo dire che tale retta è il grafico di Oppure potremmo prendere la retta che passa per il punto in alto a destra, il punto (45,70), ossia |