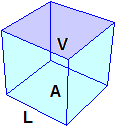
Al variare delle dimensioni di una scatola di latta cubica cambia la quantità di liquido che essa può contenere. Nella figura a sinistra le lettere L, A e V indicano il lato in cm, l'area di una faccia quadrata in cm2 e il volume in cm3 della scatola.	[clicca l'immagine per ingrandirla]
Vogliamo studiare come, al cambiare delle dimensioni del lato scatola, cambiano la superficie di una faccia e il volume della scatola stessa.
A destra sono rappresentati alcuni grafici.  I primi tre, in disordine, rappresentano come al variare del lato di base della scatola (in cm) cambiano l'altezza, l'area e il volume della scatola. Stabilisci per ogni grafico che cosa esso rappresenta (metti opportune lettere, scelte tra L, A e V, a fianco degli assi).
[attenzione:  l'altezza della scatola è uguale al suo … , quindi …]
Infine stabilisci che cosa rappresenta il quarto grafico (metti anche in questo caso opportune lettere, scelte tra L, A e V, a fianco degli assi).

[clicca l'immagine per ingrandirla]

Essendo la scatola cubica, lato ed altezza sono uguali: il terzo grafico rappresenta, dunque, come al variare del lato di base cambia l'altezza; posso mettere L sia sull'asse orizzontale che su quello verticale.     Negli altri due casi, messo L sull'asse orizzontale, devo capire in quale dei due casi sull'asse verticale devo mettere A (l'area in cm2) e in quale devo mettere V (il volume in cm3).  Se il lato è: di 5 cm, l'area di una faccia è di 25 cm2 e il suo volume è di 25·5 cm3 = 125 cm3.  Se il lato è: di 10 cm, l'area di una faccia è di 100 cm2 e il suo volume è di 100·10 cm3 = 1000 cm3.  Dunque le scelte che devo operare sono quelle indicate nella figura a lato.     Il quarto grafico non è altro che il primo, con gli assi scambiati:  esso rappresenta come deve variare L per ottenere il volume V.