Determina il baricentro di una piastra di materiale omogeneo, di forma semicircolare e di spessore costante.

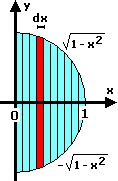
Disponiamo un semicerchio di raggio 1 nel modo illustrato a lato. Per simmetria, la ordinta yB del baricentro B è 0. Determiniamone la x. Il baricentro B è il punto in cui possiamo pensare concentrata tutta la massa per lo studio degli effetti rotatori. Quindi il momento rispetto a (0,0) di una massa concentrata in esso equivale alla somma dei momenti dovuti alle striscette verticali in cui possiamo pensare suddiviso il semicerchio. Ragioniamo sull'aree in quanto le masse (nel caso di una piastra omogenea) sono ad esse proporzionali. La striscetta di ampiezza dx e centrata in x ha area 2√(1-x2)·dx; il suo contributo al momento è x·2√(1-x2)·dx. La somma di questi contributi  ∫I2x(1-x2)1/2dx  con I = [0,1] deve eguagliare xB·AreaSemicerchio. ∫I2x(1-x2)1/2dx = -2/3*(1-12)3/2+2/3*(1-02)3/2 = 2/3 2/3 = xB·π/2   xB = 2/3·2/π = 4/(3π) (= 0.424413181578387… ma, dato il contesto, ci basta 0.4244). Più in generale, se R è il raggio del cerchio il baricentro dista 4R/(3π) dal diametro che delimita il semicerchio.

Calcolo dell'integrale con lo script "integrali" presente qui

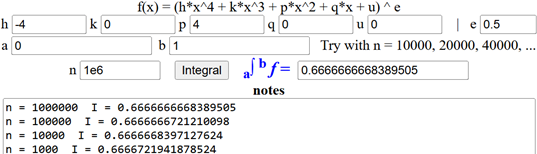
da cui deduco che l'integrale è 0.666... = 2/3.

Come potevo trovare il baricentro senza ricorrere al calcolo integrale con un programmino, qui realizzato in JavaScript:

function F(x) {return Math.sqrt(1-x*x)}
for(k=0; k<5; k=k+1) {n=Math.pow(10,k)*1e3;
X=new Array(n); Y=new Array(n)
for(i=0; i<n; i=i+1) {X[i]=-1+2/(n-1)*i; Y[i]=F(X[i])}; X[n]=-1; Y[n]=0
area = (Y[n]+Y[0])*(X[n]-X[0])
for(i=0; i<n; i=i+1) {area=area+(Y[i]+Y[i+1])*(X[i]-X[i+1])}; area = Math.abs(area)/2
document.write("n="+n+", area="+area)
CX=(X[n]+X[0])*(X[n]*Y[0]-X[0]*Y[n])
for(i=0; i<n; i=i+1) {CX=CX+(X[i]+X[i+1])*(X[i]*Y[i+1]-X[i+1]*Y[i])}
CY=(Y[n-1]+Y[0])*(X[n-1]*Y[0]-X[0]*Y[n-1])
for(i=0; i<n; i=i+1) {CY=CY+(Y[i]+Y[i+1])*(X[i]*Y[i+1]-X[i+1]*Y[i])}
document.write(", xC="+Math.abs(CX/(6*area)))
document.write(", YC="+Math.abs(CY/(6*area))+"<br>") }

n=1000,     area=1.5707436595231425, xC=1.1780227133116953e-17, YC=0.4244250952378197
n=10000,    area=1.570794663465802,  xC=2.7756258903175833e-16, YC=0.4244136029749518
n=100000,   area=1.5707962742026587, xC=3.645858173597396e-15,  YC=0.42441319545933953
n=1000000,  area=1.5707963040583859, xC=4.471912615508346e-9,   YC=0.42441318771840136
n=10000000, area=1.5707963267424758, xC=1.8030344538264895e-14, YC=0.4244131815925366

area=1.57079633 (che sappiamo essere π/2), xC=0, YC=0.42441318
a scopi pratici ce n'è d'avanzo