In un manuale scolastico si trova, sull'analisi degli errori in fisica, che se  Q = F(x1,…,xN)  è il valore di una grandezza dipendente dalle N grandezze  x1,…, xN,  e se le precisioni  Δx1,…, ΔxN  di queste sono tra loro indipendenti, allora la precisione di Q è  √( (Dx1 F(x1,…,xN)·Δx1)² + … + (DxN F(x1,…,xN)·ΔxN)² )  [DkF indica la derivazione di F rispetto alla variabile k].
    Osserviamo che nel caso in cui Q dipenda da una sola grandezza la formula si riduce alla espressione del valore assoluto del differenziale di F, ossia di  dF(x) = Dx(F(x))·Δx.
    Si fa l'esempio:  Q = A·B/C,  A = 10±2,  B = 30±2,  C = 20±1;   Q = 10·30/20 = 15,
ΔQ = √( (30/20·2)² + (10/20·2)² + (−10·30/20²·1)² ) = 3.25,  per cui si avrebbe  Q = 15 ± 3.25.
    Discuti quanto presentato da questo libro.

    Facciamo due conti.  I "calcoli" del libro sono giusti:
con WolframAlpha  sqrt((30/20*2)^2+(10/20*2)^2+(-10*30/20^2*1)^2)  → 3.25
    Vediamo se è corretto il loro uso.
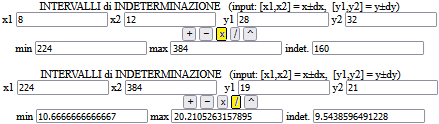
Approssimazione per difetto:  (10-2)*(30-2)/(20+1) = 32/3 = 10.66667
Per eccesso:  (10+2)*(30+2)/(20-1) = 384/19 = 20.21053
    Posso prendere come intervallo di indetreminazione  [10.66, 20.22].
    Ovvero calcolo il centro tra questi due valori e il raggio:
((10+2)*(30+2)/(20-1) + (10-2)*(30-2)/(20+1)) / 2; ( (10+2)*(30+2)/(20-1) - (10-2)*(30-2)/(20+1) ) / 2
15.4386,  4.77193
15.44 ± 4.78  (o  15.4 ± 4.9)

    L'intervallo di indeterminazione ottenuto dal libro,  15 ± 3.25 = [11.75, 18.25], è errato:  è molto più piccolo (e "scentrato") rispetto a  15.44 ± 4.78 = [10.66, 20.22]

    La formula che propone il libro può essere usata solo per "approssimare" la deviazione standard di Q a partire da quelle di x1,…, xN, e sotto opportune ipotesi, che qui non discutiamo. Essa appare certamente come una cosa "magica" al lettore, quando deve affrontare un esercizio che potrebbe risolvere più correttamente e in modo comprensibile in altro modo!

    I calcoli, più semplici, usando lo script "calcolo approssimato" presente qui, tenendo conto che A, B e C stanno in [8,12], [28,32], [19,21]:


8 12 * 28 32 = 224 384 | 160
[ 304 +/- 80 ]
224 384 / 19 21 = 10.6666666666667 20.2105263157895 | 9.5438596491228
[ 15.4385964912281 +/- 4.7719298245614 ]

    O col software online www.wolframalpha.com. Vedi qui.
minmax x*y/z if( 10-2<x<10+2 and 30-2<y<30+2 and 20-1<z<20+1 )
      min ≈ 10.6667 at (x, y, z) = (8, 28, 21)
      max ≈ 20.2105 at (x, y, z) = (12, 32, 19)