Ho la fotografia multiflash (uno scatto ogni 30-esimo di secondo) di una palla da biliardo lasciata cadere da una certa posizione, a fianco ad un metro graduato con tacche ampie un millimetro. Cliccando puoi ingrandire la foto (che per comodità è stata ruotata di 90°). Rappresenta graficamente il fenomeno e cerca di dedurne, con opportune elaborazioni, l'andamento (lo "0" del metro non corrisponde al punto esatto da cui è stata lasciata cadere la bilia).

Posso ritenere "esattamente" di 1/30 di secondo gli intervalli di tempo tra uno scatto e il successivo, mentre devo valutare in modo opportunamente approssimato le posizioni della pallina. Dalle foto riesco a valutare le posizioni arrotondate al mezzo millimetro. Riferendosi alle posizioni segnate con le tacche, individuandone le coordinate in centimetri, abbiamo:

9.5, 15, 21.5, 29.5, 38.5, 48.5, 59.5, 71.5, 85, 99, 114, 130.5, 148, 167

ovvero, in metri:

0.095, 0.15, 0.215, 0.295, 0.385, 0.485, 0.595, 0.715, 0.85, 0.99, 1.14, 1.305, 1.48, 1.67

Rappresento questi dati nel piano x,y con x 1/30, 2/30, ..., 14/30 e y 0.095, 0.15, ..., 1.67. Vedi il grafico sottostante a sinistra (realizzato con questo script):

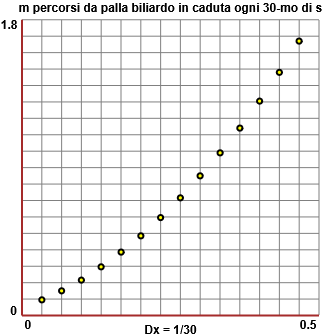
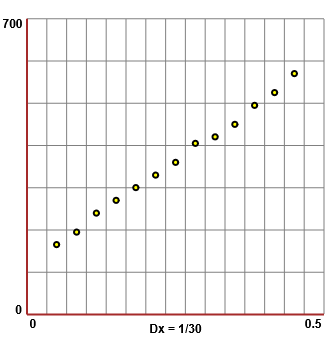
Per capire come "sale" la curva lungo cui tendono a disporsi i punti calcolo e rappresento graficamente a partire dal seconto punto la differenza tra l'ordinata e l'ordinata del punto precedente, ossia (dato che le ordinate rappresentano le altezze) la velocità media in ogni intervallino di tempo con cui cade la palla. Vedi il grafico soprastante a destra (realizzato con questo script).

Vedo che i punti tendono a disporsi lungo una retta: la velocità di caduta della palla cresce linearmente. Se so che la pendenza del grafico di una funzione polinomiale di 2º grado varia linearmente, posso dedurne che il fenomeno studiato ha andamento parabolico.
Posso comunque studiare il fenomeno cercando di trovare l'equazione polinomiale di 2º grado che meglio approssima i dati. Posso utlizzare lo script "regressione quadratica" accessibile da qui.

x:
0.033333333, 0.066666667, 0.1, 0.133333333, 0.166666667, 0.2, 0.233333333, 0.266666667, 0.3, 0.333333333, 0.366666667, 0.4, 0.433333333, 0.466666667
y:
0.095, 0.15, 0.215, 0.295, 0.385, 0.485, 0.595, 0.715, 0.85, 0.99, 1.14, 1.305, 1.48, 1.67

Ottengo: y = 4.8368818619610016*x^2 + 1.2125480792101565*x + 0.04793956032642456
ovvero: y = 4.837*x*x + 1.2125*x + 0.0479

Sovrapponendo al primo grafico questa curva, con questo script, trovo un'ottima corrispondenza:

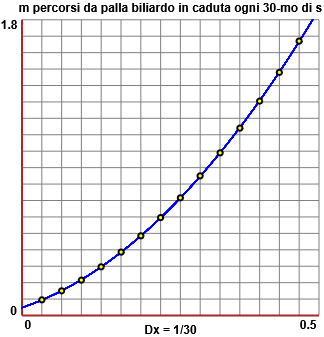
La sequenza 0.033333333, 0.066666667, 0.1, ..., 0.5 è stato ottenuta con lo script "numeri/sequenze" presente qui introducendo "tra 0.03333333333 e 0.5, passo 0.03333333333".

Esaminiamo i dati con WolframAlpha (vedi). Utilizziamo i tempi in 30-esmi di secondo e lo spazio in centimetri.

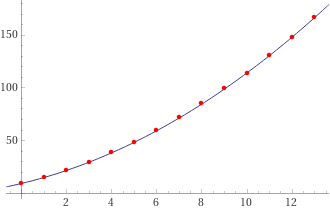
quadratic fit {(0,9.5),(1,15),(2,21.5),(3,29.5),(4,38.5),(5,48.5),(6,59.5),(7,71.5),(8,85),(9,99),(10,114),(11,130.5),(12,148),(13,167)} y = 0.537431 x^2 + 5.11669 x + 9.37321

Si trova, come sopra, che è ottima l'approssimazione con una funzione quadratica. Si potrebbe poi cambiare unità di misura e arrivare ad una funzione simile a quella trovata in precedenza.