1.2,1.5,1.8,2.2,2.5,2.8,3.1, 3.4, 3.7, 4.1, 4.4, 4.7, 5.0,
5.3, 5.6, 6.0, 6.3, 6.6, 6.9,7.2,7.6,7.9,8.2,8.5,8.8,9.1
0.8,2.6,4.2,6.0,7.3,8.4,9.4,10.3,11.0,11.8,12.2,12.5,12.7,
12.7,12.6,12.3,11.9,11.4,10.7,9.9,8.7,7.6,6.4,5.0,3.5,1.9
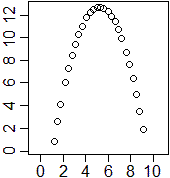
| Ho la fotografia multiflash di una palla lanciata in aria. Gli intervalli di tempo tra due immagini successive sono uguali. Non ho informazioni sui valori effettivi delle distanze spaziali e temporali, per cui con una riga graduata rilevo le distanze, in centimetri, delle posizioni del centro della palla dal margine sinistro e dal margine basso della foto. Ecco, in ordine, le "ascisse" e le "ordinate" dei punti così determinate: |  |
1.2,1.5,1.8,2.2,2.5,2.8,3.1, 3.4, 3.7, 4.1, 4.4, 4.7, 5.0,
5.3, 5.6, 6.0, 6.3, 6.6, 6.9,7.2,7.6,7.9,8.2,8.5,8.8,9.1
0.8,2.6,4.2,6.0,7.3,8.4,9.4,10.3,11.0,11.8,12.2,12.5,12.7,
12.7,12.6,12.3,11.9,11.4,10.7,9.9,8.7,7.6,6.4,5.0,3.5,1.9
|
Possiamo ritenere le misure approssimate a meno di 1 mm. Come si può trovare, utilizzando il computer per elaborare i dati, quale tipo di curva ha descritto la palla?
Ecco tre immagini, A, B e C, che descrivono un procedimento che si può seguire:
Ora spigheremo e commenteremo immagini e procedimento.
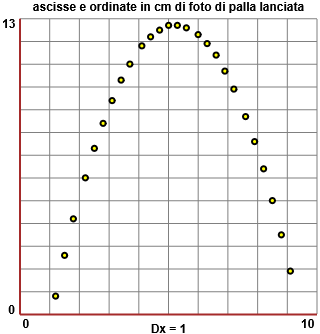
Il grafico A rappresenta i dati. Lo abbiamo ottenuto con questo script (abbiamo scelto l'intervallo delle x e quello delle y tenendo conto dei dati). I punti sembrano disporsi lungo una parabola. Per studiare meglio la situazione ci conviene usare gli script presenti qui. Incominciamo ad usare "differenze", per calcolare le differenze tra due successive "y": se le differenze fossero più o meno costanti i punti di A sarebbero disposti lungo una retta, cosa ovviamente non vera; se le differenze fossero crescenti o decrescenti in modo proporzionale i punti di A avrebbero andamento parabolico; se le differenze variassero in modo parabolico i punti avrebbero un andamento cubico; ...

Introduco:
Ottengo:
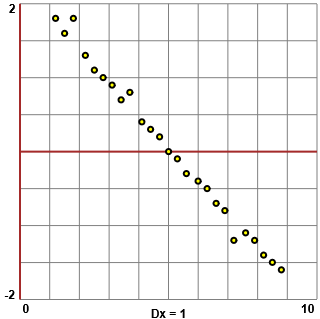
Rappresento queste differenze graficamente con questo script ottenendo la figura B (ho scelto l'intervallo delle y tenendo conto dei valori ottenuti, tra -1.6 e 1.8). I punti sono quasi allineati. Deduco che i dati iniziali (rappresentati in A) hanno andamento parabolico.
A questo punto cerco la funzione polinomiale di 2º grado che approssima al meglio i dati con lo script "regressione quadratica".

x:
1.2,1.5,1.8,2.2,2.5,2.8,3.1,3.4,3.7,4.1,4.4,4.7,5.0,5.3,5.6,6.0,6.3,6.6,6.9,7.2,7.6,7.9,8.2,8.5,8.8,9.1
y:
0.8,2.6,4.2,6.0,7.3,8.4,9.4,10.3,11.0,11.8,12.2,12.5,12.7,12.7,12.6,12.3,11.9,11.4,10.7,9.9,8.7,7.6,6.4,5.0,3.5,1.9
Ottengo: y = -0.7260205120093551*x^2 + 7.607383731383213*x - 7.203617752521756
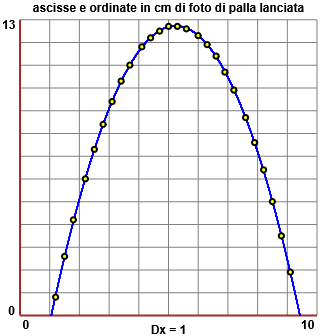
La figura C è stata ottenuta con questo script in cui si è
introdotta la funzione
y =
Come si vede c'è un ottimo accordo tra punti sperimentali e curva descritta da questa equazione: la palla ha
un andamento parabolico.