km: 0, 1, 2, 4, 6, 8, 10, 15, 20, 30 atm: 1,0.886,0.785,0.608,0.465,0.35,0.26,0.115,0.069,0.012
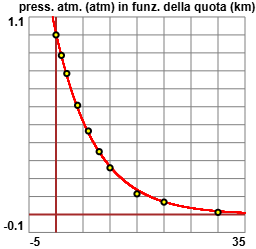
La pressione atmosferica è influenzata da vari fattori ma, mediamente,
al variare della quota sul livello del mare ha un andamento abbastanza regolare.
Qui sotto sono riportati i valori medi, rispetto al tempo e alla zona
geografica, della pressione in atmosfere in corripondenza dell'altitudine in km
rilevati dalla NASA. A destra i dati sono riportati
su un sistema di assi ed è tracciato il grafico di una funzione che
li approssima. Prova a trovare la funzione. Se vuoi utilizza uno script (tra quello presenti sul sito) o WolframAlpha.km: 0, 1, 2, 4, 6, 8, 10, 15, 20, 30 atm: 1,0.886,0.785,0.608,0.465,0.35,0.26,0.115,0.069,0.012 |  |
Prima usiamo WolframAlpha (vedi). Poi vedremo come usare altro software.
Proviamo con una funzione quadratica:
quadratic fit (0,1),(1,0.886),(2,0.785),(4,0.608),(6,0.465),(8,0.35),(10,0.26),(15,0.115),(20,0.069),(30,0.012)
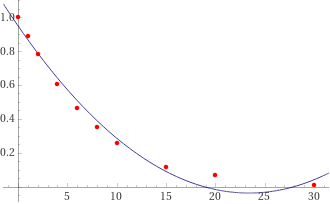
0.00179858 x^2 - 0.0840002 x + 0.947369
Evidentemente questa scelta è da scartare.
Proviamo con una funzione cubica:
cubic fit (0,1),(1,0.886),(2,0.785),(4,0.608),(6,0.465),(8,0.35),(10,0.26),(15,0.115),(20,0.069),(30,0.012)
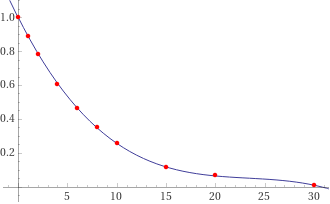
-0.0000690156 x^3 + 0.00481989 x^2 - 0.115345 x + 0.998035
Anche questa scelta è da scartare: non può scendere sotto all'asse x.
Proviamo con una funzione esponenziale:
exp fit (0,1),(1,0.886),(2,0.785),(4,0.608),(6,0.465),(8,0.35),(10,0.26),(15,0.115),(20,0.069),(30,0.012)
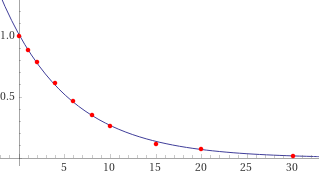
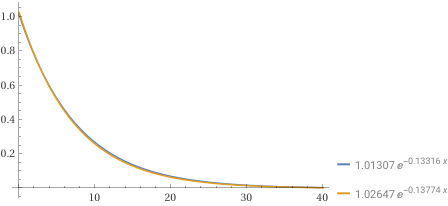
1.01307 e^(-0.13316 x)
Ottima approssimaziome. Posso prendere x → 1.01*exp(-0.133*x).
Ecco come si potevano utilizzare gli script "regressione" presenti qui (e gli script per tracciare grafici accessibili da qui):
|
Con "regressione quadratica" ottengo: | 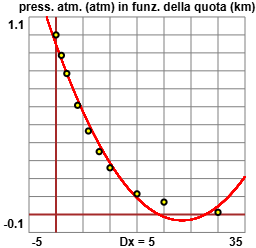 |
Con "regressione cubica" ottengo, analogamente: | 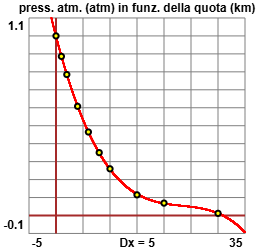 |
Con "regressione esponenziale" ottengo, analogamente: |  |
QUI lo script con cui sono stati fatti i 3 grafici nella stessa scala.
Sotto con WolframAlpha la verifica che le due formulazioni della funzione esponenziale trovate nei due modi sono
sostanzialmente equivalenti: