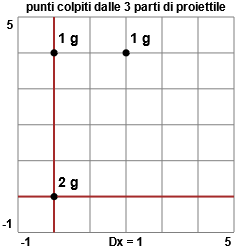
Un proiettile esplosivo di massa pari a 4 g viene sparato contro un bersaglio. Prima di colpire il bersaglio il proiettile si divide in tre parti di massa m₁ = 2 g, m₂ = m₃ = 1 g. Le tre parti colpiscono il bersaglio in tre punti diversi, che sul piano del bersaglio hanno rispettivamente coordinate cartesiane (0,0), (0,4) e (2,4).  Se il proiettile non fosse esploso, in quale punto avrebbe colpito il bersaglio?

A) Nel baricentro del triangolo che ha per vertici (0, 0), (0, 4) e (2, 4)
B) Nel punto (0.5, 2)
C) Nel punto (2, 0.5)
D) Nel punto (2/3, 8/3)
E) Non è possibile stabilirlo se non si conosce il punto dell'esplosione

Facciamo una figura per capire meglio il problema. Rappresentiamo le parti del proiettile.

     

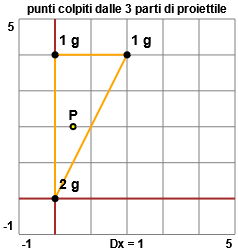
È chiaro che il punto colpito non è il baricentro del triangolo, in quanto procedendo in questo modo non si terrebbe conto che le masse dei tre vertici non sono eguali; la risposta A è da escludere.  È da escludere anche C in quanto il punto (2,0.5) non sta neanche nel triangolo.  Per scegliere tra gli altri due punti, abbastanza vicini tra loro, conviene ragionare:  se fossero tre masserelle collegate tra loro da una struttura di peso trascurabile, il baricentro sarebbe il punto per cui far passare un'asta nella struttura in modo tale che essa abbia un equlibrio stabile; capisco subito che il punto deve avere ordinata pari a 2, in quanto avremmo una massa complessiva di 2 grammi sia sopra che sotto alla ordinata 2.  Quindi la risposta corretta è la B.
Potevo procedere anche in modo pedestre, facendo i conti: se ho le masse m1, m2, m3 aventi ascisse x1, x2, x3 e ordinate y1, y2, y3, il baricentro (h,k) è (vedi):
  h = (x1·m1 + x2·m2 + x3·m3) / (m1 + m2 + m3) = (0+0+2*1)/4 = 0.5,
  k = (y1·m1 + y2·m2 + y3·m3) / (m1 + m2 + m3) = (0+4*1+4*1)/4 = 2.

Calcoli col semplice script online "baricentro2" presente qui. Grafici realizzati con questo script.