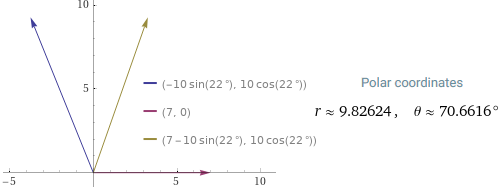F1 e F2 sono due forze con intensità di 10.00 kg e 7.00 kg.
Le loro direzioni formano un angolo di 112.0°. Qual è l'intensità di
|
Osserviamo che abbiamo espresso le forze in kg. Stiamo sottintendendo che si tratti di chilogrammi-forza (9.80665 N:
vedi), come spesso si fa nelle applicazioni. Comunque la soluzione del nostro problema è indipendente
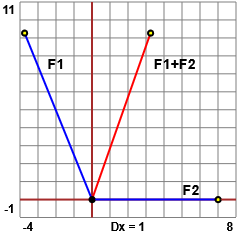
dalla unità di misura dei pesi che si impiega. Prima di metterci a fare i calcoli, rappresentiamo graficamente il problema e stimiamo le soluzioni. Ci conviene tracciare F2 orizzontalmente. Dal grafico capiamo che l'angolo è compreso tra 60° e 80° e che l'intensità di F1+F2 è circa quella di F1 (10 kg). Facciamo calcoli e grafici col software online WolframAlpha (vedi), ma potremmo usare altro software. |  |
vector(cos(112°)*10,sin(112°)*10), vector(cos(0°)*7,sin(0°)*7), vector(cos(112°)*10+cos(0°)*7, sin(112°)*10+sin(0°)*7)
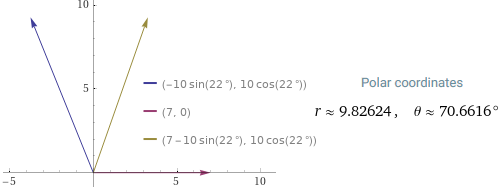
Tenendo conto che il dato "peggiore" è arrotondato a 3 cifre
(7.00), arrotondo a 3 cifre gli esiti:
Il grafico è stato tracciato con questo script
Non è banale determinare con precisione l'indeterminazione del risultato. Un modo molto semplice, che vale in generale, è ricorrere a un programmino che proceda facendo variare casualmente gli input nell'intervallo di indetermimazione, ad esempio facendo variare la prima direzione (espressa in °) tra 112-0.05 e 112+0.05 aggiungendo a 112 un numero casuale tra -0.05 e 0.05. Ecco il programmino, espresso in JavaScript, il linguaggio di programmazione più diffuso (vedi), tenendo conto che la lunghezza del vettore è:
√( (cos(112°)·10 + cos(0°)·7)² + (sin(112°)·10 + sin(0°)·7)² )
with (Math) {
min=1e50; max=-1e50
X=112; ex=0.05; Z=10; ez=0.005; Y=0; ey=0.05; W=7; ew=0.005
for(i=1; i<1e6; i=i+1)
{x=X+ex*(random()*2-1); z=Z+ez*(random()*2-1); y=Y+ey*(random()*2-1); w=W+ew*(random()*2-1)
f = sqrt( pow(cos(x*PI/180)*z+cos(y*PI/180)*w,2) + pow(sin(x*PI/180)*z+sin(y*PI/180)*w,2) )
if(f < min) min=f; if(f > max) max=f }
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2)
}
with (Math) {
min=1e50; max=-1e50
X=112; ex=0.05; Z=10; ez=0.005; Y=0; ey=0.05; W=7; ew=0.005; k=PI/180
for(i=1; i<1e6; i=i+1)
{x=X+ex*(random()*2-1); z=Z+ez*(random()*2-1); y=Y+ey*(random()*2-1); w=W+ew*(random()*2-1)
a=atan( (sin(x*k)*z+sin(y*k)*w) / (cos(x*k)*z+cos(y*k)*w) )
if(a < min) {min=a}; if(a > max) {max=a} }
min=min/k; max=max/k
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2,"<br>")
}
Output:
min=9.809832351300528 max=9.84254569884064 9.826189025070583 +/- 0.016356673770055785 min=70.56597202819987 max=70.75472485184872 70.6603484400243 +/- 0.09437641182442746
Posso concludere che l'intensità della forza complessiva varia da 9.81 a 9.85 kg, ovvero che è
9.83±0.02 kg, e che la direzione (in °) varia da 70.56 a 70.76,
ovvero che è (70.66±0.10)°.