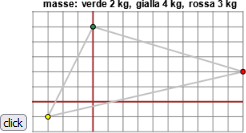
Questo script genera la disposizione di tre masse e la visualizzazione del loro valore (in chilogrammi).  L'unità di misura delle lunghezze è il metro.  Determina la posizione del centro di massa.  Controlla la risposta premendo [click] .

Ecco che cosa si otterrebbe nel caso della figura nel testo dell'esercizio:

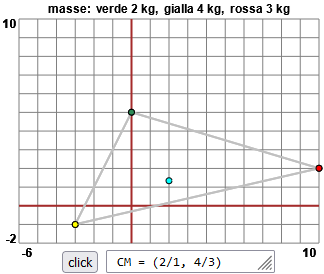
Il centro di massa è (2, 4/3).  Come si determina?
Se ho le masse m1, m2, m3, … aventi ascisse x1, x2, x3, … e ordinate y1, y2, y3, …, il baricentro (h,k) è:
    h = (x1·m1 + x2·m2 + x3·m3 + …) / (m1+m2+m3+ …)
    k = (y1·m1 + y··m2 + y3·m3 + …) / (m1+m2+m3+ …).
Nel nostro caso:
    h = (0*2+(-3)*4+10*3)/(2+4+3) = 18/9 = 2,  k = (5*2+(-1)*4+2*3)/(2+4+3) = 12/9 = 4/3

Questo esercizio online può essere usato dagli studenti per autoesercitarsi o dal docente per copiare immagini da assegnare per compiti in classe, di cui può conrollare le risposte usando lo script "baricentro2" presente QUI.

Per altri commenti: figure(2) neGli Oggetti Matematici.