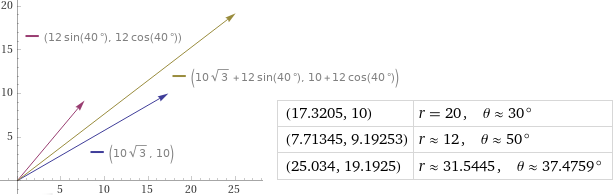
(arrotondo la lunghezza del vettore a 31.5±1 e la sua direzione a 37.5±1°)
Qual è la forza complessiva esercitata da due forze, una di 20 N con direzione 30°, l'altra di 12 N con direzione di 50°. Tieni conto che le grandezze (intensità e direzioni) sono espresse con due cifre significative.
Devo considerare il vettore ( cos(30°)·20 + cos(50°)·12, sin(30°)·20 + sin(50°)·12 ).
Calcoli e grafici col software online WolframAlpha (vedi).
Vedremo poi come procedere altrimenti.
vector(cos(30°)*20,sin(30°)*20), vector(cos(50°)*12,sin(50°)*12), vector(cos(30°)*20+cos(50°)*12,sin(30°)*20+sin(50°)*12)

Tenendo conto dell'indeterminazione dei dati di partenza posso ritenere le precisioni di circa 1 N e 1°. Per valutazioni più precise vedi sotto.
Nota. In qualche libro di fisica per un problema come questo si trovano le soluzioni 37.5 e 31.5 con 3 cifre significative. Ma, in questo caso, le cifre significative non sono neanche 2! (anche se i dati iniziali avessero 3 cifre significative - ossia se le forze avessero la precisione di 5 grammi-peso e le direzioni di 0.05° - non avremmo neanche 3 cifre significative).
Non è banale determinare con precisione l'indeterminazione del risultato. Un modo molto semplice, che vale in generale, è ricorrere a un programmino che proceda facendo variare casualmente gli input nell'intervallo di indetermimazione, ad esempio facendo variare la prima direzione (espressa in °) tra 30-0.05 e 30+0.05 aggiungendo a 30 un numero casuale tra -0.05 e 0.05. Ecco il programmino, espresso in JavaScript, il linguaggio di programmazione più diffuso (vedi), tenendo conto che la lunghezza del vettore è:
√( (cos(30°)·20 + cos(50°)·12)² + (sin(30°)·20 + sin(50°)·12)² )
with (Math) {
min=1e50; max=-1e50
X=30; ex=0.5; Z=20; ez=0.5; Y=50; ey=0.5; W=12; ew=0.5
for(i=1; i<1e6; i=i+1)
{x=X+ex*(random()*2-1); z=Z+ez*(random()*2-1); y=Y+ey*(random()*2-1); w=W+ew*(random()*2-1)
f = sqrt( pow(cos(x*PI/180)*z+cos(y*PI/180)*w,2) + pow(sin(x*PI/180)*z+sin(y*PI/180)*w,2) )
if(f < min) min=f; if(f > max) max=f }
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2)
}
with (Math) {
min=1e50; max=-1e50
X=30; ex=0.5; Z=20; ez=0.5; Y=50; ey=0.5; W=12; ew=0.5; k=PI/180
for(i=1; i<1e6; i=i+1)
{x=X+ex*(random()*2-1); z=Z+ez*(random()*2-1); y=Y+ey*(random()*2-1); w=W+ew*(random()*2-1)
a=atan( (sin(x*k)*z+sin(y*k)*w) / (cos(x*k)*z+cos(y*k)*w) )
if(a < min) {min=a}; if(a > max) {max=a} }
min=min/k; max=max/k
document.write("min=",min," max=",max,"<br>")
document.write(min+(max-min)/2," +/- ", (max-min)/2,"<br>")
}
Output:
min=30.527160653763442 max=32.56136207882207 31.54426136629276 +/- 1.0171007125293148 min=36.68449658622853 max=38.27188156830901 37.47818907726877 +/- 0.7936924910402396
Posso concludere che l'intensità della forza complessiva varia da 30.5 a 32.6 N, ovvero che è 31.5±1.1 N, e che la direzione (in °) varia da 36.6 a 38.3, ovvero che è 37.5±0.9 °.
La rappresentazione grafica con questo script:
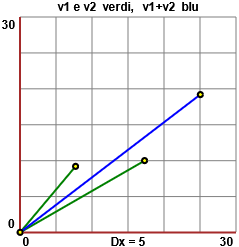
Per altri commenti:
 calcolo approssimato neGli Oggetti Matematici
calcolo approssimato neGli Oggetti Matematici