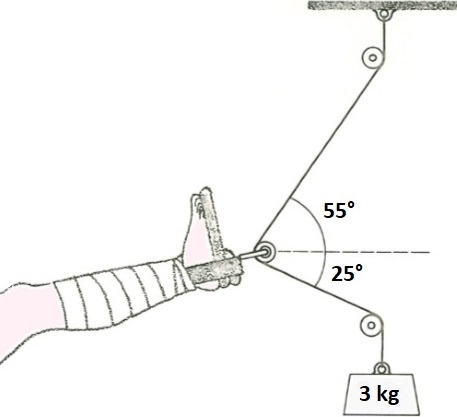
La forza che il dispositivo di trazione raffigurato a fianco esercita sul piede del paziente può essere maggiore di 3 kg?  Quanto vale?

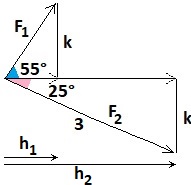Nella figura a fianco abbiamo rappresentato con F1 ed F2 le due trazioni della fune e con k le loro componenti verticali, della stessa intensità ma di direzioni opposte.  Devo determinare h1+h2. Sapendo che F2 è di 3 kg, posso determinare k.  Indico con "degrees" π/180. k = 3*sin(25*degrees);   quindi: h2 = 3*cos(25*degrees);   determiniamo h1: h1 = cos(55*degrees)*F1;  F1*sin(55*degrees) = k;   quindi: h1 = cos(55*degrees)*k/sin(55*degrees);   concludendo; h1;  h2;   h1+h2 0.8877615; 2.718923; 3.606685     Arrotondo a  3.6 (kg)

La forza complessiva è maggiore di quella esercitata dalla massa appesa: oltre a questa forza infatti interviene anche quella esercitata dal soffitto, che trattiene la parte superiore del cavo. La somma delle due forze viene poi ridotta a causa degli angoli (al diminuire di 55° e di 25° la somma delle due forza aumenta di intensità; quando arrivano a 0° la forza di trazione è di 6 kg).

I calcoli posso farli facilmente con WolframAlpha (vedi sotto) o con una della calcolatrici (ad esempio quella "piccolissima") presenti qui:

Metto in A 3*Math.cos(25*Math.PI/180)  clicco [=] e ho 2.7189233611  (h2)
In A Math.cos(55*Math.PI/180)*3*Math.sin(25*Math.PI/180)/Math.sin(55*Math.PI/180), [=], ho 0.887761478 (h1)
In A  2.7189233611 + 0.887761478,  [=]  e ho  3.6066848391
Se prima avessi messo 1 in D avrei avuto   3.6

Con "calcolatrice2" basta mettere (sopra a B)  3*sin(25*PI/180)*cos(55*PI/180)/sin(55*PI/180)+3*cos(25*PI/180)  per avere 3.60668483907…

ConWolframAlfha:
3*sin(25°)*cos(55°)/sin(55°) + 3*cos(25°)       3.60668483907771567...
rouund( 3*sin(25°)*cos(55°)/sin(55°) + 3*cos(25°), 0.1)       3.6