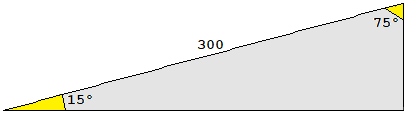
La figura a destra illustra la forza che il muscolo deltoide esercita sull'omero. Da studi con i raggi X si è trovato che quando il baccio è orizzontale questa forza è inclinata di circa 15° rispetto all'omero. Supponendo che l'intensità di questa forza sia di 300 N, determinane la componente diretta come l'omero (che ha la funzione di sostenere il braccio) e quella diretta perpendicolarmente ad esso (che ha la fuzione di bloccare l'articolazione tirando l'omero verso la scapola).

Possiamo procedere in vari modi. Ad esempio possiamo tracciare la figura su carta quadrettata (o millimetrata) usando un goniometro, come nella figura sottostante, tracciando il lato orizzontale lungo 10, e trovare che quello verticale è circa 2.7. Con il righello o con il teorema di Pitagora troviamo l'ipotenusa (sqrt(2.7^2+10^2) = 10.35808…), che approssimiamo a 10.4.

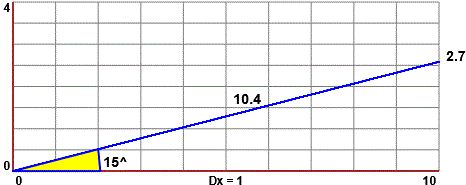
A questo punto possiamo ricavare la componente orizzontale e quella verticale della forza tenendo conto che queste forze si dispongono come i due cateti del triangolo rettangolo (di lati 10, 2.7 e 10.4) sopra disegnato.
ForzaOrizzonatale = 300 N ·10/10.4 = 288.46… che arrotondo a 290 N
ForzaVerticale = 300 N ·2.5/10.4 = 77.884… che arrotondo a 78 N

Oppure potremmo tracciare un triangolo rettangolo della stessa forma ma con l'ipotenusa lunga 10, ricavare graficamente (senza uso del teorema di Pitagora) i cateti orizzontale e verticale e procedere in modo simile.

Quando conoscerai le funzioni trigonometriche potrai procedere più rapidamente (ForzaVerticale = 300 N · sin(15°) = 77.645… N, che arrotondo a 78 N; ForzaOrizzontale = 300 N · cos(15°) = 289.777… N, che arrotondo a 290 N).

Volendo, ecco come fare i calcoli con lo script "tri ang-lato-ang" presente qui:

Per altri commenti: vettori neGli Oggetti Matematici.

Se vuoi vedere come è stato tracciato il triangolo rettangolo iniziale vedi QUI.