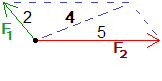
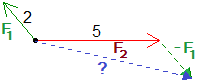
Sappiamo che le forze F1 e F2 sono applicate allo stesso punto e che hanno intensità di, rispettivamente, 2 e 5 chilogrammi. Sappiamo la che loro somma ha intensità di 4 kg.  Qual è l'intensità della loro differenza?  [esercizio non facile; prova a risolverlo e poi guarda la soluzione]

Il problema può essere risolto con tecniche algebriche, in vari modi, ma forse il modo più semplice di affrontarlo è quello di aiutarsi col disegno, cercando prima di stimare il valore della soluzione. Innanzi tutto capiamo che l'angolo tra le direzioni di F1 e di F2 deve essere maggiore di 90° in quanto la loro somma ha intensità minore di quella di F2.  Deduciamo, anche, che il vettore differenza F2−F1 (quello indicato col "?") deve avere intensità maggiore del vettore somma.

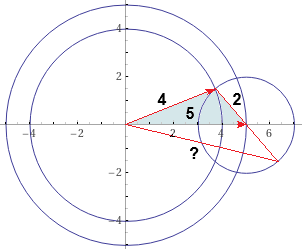
Aiutandoci col computer illustriamo la situazione: disegno un cerchio di raggio 5 ed uno di raggio 4 centrati nell'origine, ed uno di raggio 2 centrato in (5,0). Sotto a destra la figura ottenuta con WolframAlpha col comando:  circle (-5,0),(5,0),(0,5), circle (-4,0),(0,4),(0,4), circle (3,0),(7,0),(5,2).  Alla immediata sinistra di questa, quella ottenibile col comando:  (x^2+y^2-16)*((x-5)^2+y^2-4)*(x^2+y^2-25)=0  che fornisce anche le coordinate dei punti di intersezione,  che potevo comunque trovare con  x^2+y^2=16, (x-5)^2+y^2=4  e con  x^2+y^2=25, (x-5)^2+y^2=4.

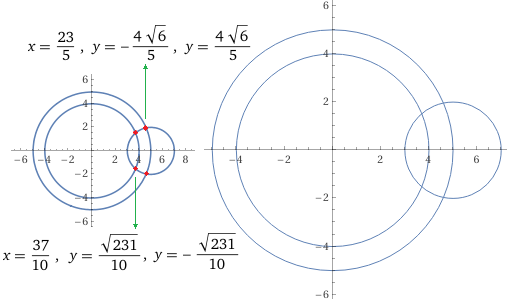Il vettore ? termina nel simmetrico di (3.7, √231/10) rispetto a (5,0), ossia in x = 6.3, y = -√231/10;  è dunque lungo √(6.3^2+2.31) = √42 = 6.480740698...  Questo è il modulo di F2−F1.

I calcoli, sopra fatti con l'aiuto del computer, potevano essere fatti senza di esso.