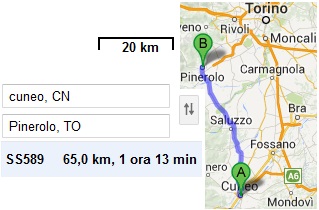
Da un sito per valutare il percorso stradale per raggiungere una località da un'altra località si ottiene quanto riprodotto a lato. Quale sarebbe la velocità media di un'auto che percorresse questo tratto di strada nel modo indicato? (tieni conto che i valori indicati sono arrotondati)
Consideriamo le approssimazioni per difetto ed eccesso di spazio e tempo e utilizziamole per trovare quelle della velocità: t1 <- 1+12.5/60; t2 <- 1+13.5/60 s1 <- 64.95; s2 <- 65.05 v1 <- s1/t2; v2 <- s2/t1; c(v1,v2) #   53.02041   53.83448

La velocità è compresa tra 53.02041 km/h e 53.83448 km/h, o, più in breve, tra 53 km/h e 54 km/h, ovvero 53.5±0.5 km/h (ovvero 53 km/h è l'approssimazione per troncamento)

  Per altri commenti: calcolo approssimato neGli Oggetti Matematici.

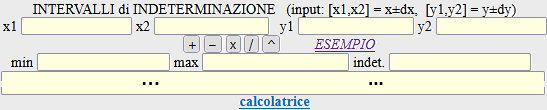
Volendo, capito come procedere "a mano", si possono far eseguire i calcoli dal computer, ad esempio con lo script "calcolo approssimato" accessibile da qui (usando anche la calcolatrice incorporata):

Concludendo: 53.43 ± 0.41 o meglio 53.5 ± 0.5

Posso anche utilizzare il software online www.wolframalpha.com; vedi qui:
minmax x/y where abs(x-65)<0.05 and abs(y-(1+13/60))<0.5/60
      max ≈ 53.8345 at (x, y) ≈ (65.05, 1.20833)
      min ≈ 53.0204 at (x, y) = (64.95, 1.225)