H (mm) F (g) 11 220 16 350 30 590 47 940

Per studiare le caratteristiche di un elastico, lo si tiene sospeso per un estremo e si appendono all'altro estremo diversi oggetti. Ogni volta si misura il peso dell'oggetto e il corrispondente allungamento dell'elastico.  Il peso F degli oggetti viene misurato con una bilancia a molla con divisioni di 10 g (in modo che se l'ago si ferma vicino alla tacca 220 si può assumere che il peso sia 220±5 g). Le lunghezze che assume l'elastico vengono misurate con la precisione di 1 mm, in modo che i valori dell'allungamento H (ottenuti come differenza di due lunghezze) hanno la precisione di 2 mm. Si ottengono i valori riportati nella tabella a fianco.     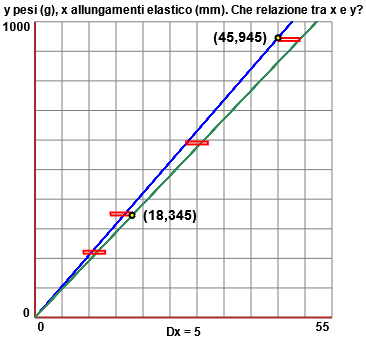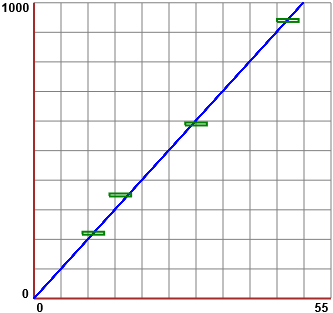Ipotizzando che, nell'intervallo di valori considerato, la relazione tra lunghezza dell'elastico e peso sia lineare, trova k tale che F=H·k.

    Sotto sono indicati altri due possibili procedimenti.

(a)   Rappresentare i rettangoli che sono il prodotto degli intervalli di indeterminazione delle varie coppie di dati e trovare graficamente un intervallo di indeterminazione per k (si cercano le rette passanti per (0,0) e per tutti i rettangolini di minima e di massima pendenza). 345 —— 18  = 115/6 = 19.17 ≈ 19   945 —— 45  = 21   19 ≤ k ≤ 21   cioè k = 20±1 (b)   Calcolare gli intervalli di indeterminazione dei valori F/H relativi alle quattro prove, cioè: [215/13,225/9] = [16.538…,25], [345/18,355/14] = [19.166…,25.357…], … e farne l'intersezione.     Si riottiene, ovviamente, lo stesso intervallo ottenuto con il metodo (a).

(b)   Calcolare gli intervalli di indeterminazione dei valori F/H relativi alle quattro prove, cioè: [215/13,225/9] = [16.538…,25], [345/18,355/14] = [19.166…,25.357…], … e farne l'intersezione.

    Si riottiene, ovviamente, lo stesso intervallo ottenuto con il metodo (a).

Ecco come è stata ottenuta l'immagine precedente con uno script: vedi QUI.       Se non avessimo conosciuto le precisioni delle misure di H e di F avremmo potuto procedere con il calcolo della regressione vincolata a passare per (0,0)  (vedi il programma "retta regressione" qui)  ottenendo F = 20.052*H, senza informazioni sulla precisione di 20.052.