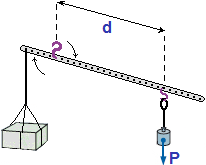
Sappiamo che per spingere una porta se ci si avvicina all'asse di rotazione si deve esercitare una forza maggiore. Facciamo un esperimento per studiare meglio il fenomeno. Prendete un'asta metallica forata e, come illustrato a destra, fissate ad una estremità un oggetto abbastanza pesante, sospendete l'asta con un gancio posto a qualche foro di distanza da tale estremità. Appendete dall'altra parte con un piccolo gancetto (potrebbe essere anche una graffetta metallica) un altro oggetto di cui potete far variare il peso, ad esempio una bottiglia di plastica contenente acqua tenuta sospesa con uno spago chiuso ad anello. Fissate il gancetto a varie distanze d e versate dell'acqua nella bottiglia fino a che l'asta raggiunge la posizione orizzontale. Ogni volta pesate la bottiglia con una bilancia da cucina e annotate i valori d e P.  Rappresentate, infine, su un grafico i valori di d (approssimati ai millimteri) e di P (approssimati ai grammi), e calcolate i vari prodotti P·d. Che cosa osservate?

Come misurare i valori di d? Supponiamo di usare un'asta contenente 25 fori. Misuariamo la distanza tra il primo e l'ultimo foro. Supponiamo di ottenere 30.0 cm. Posso dedurre che la distanza tra un foro e l'altro è 30 cm / 24 = 1.25 cm. Possiamo ritenere le misure delle distanze praticamente esatte. Le misure dei pesi di bottiglia+spago+acqua saranno meno precise. Supponiamo che abbiano la precisione di 10 g. Ipotizziamo di ottenere i valori ("d" sono le distanze tra i fori, "p" sono i pesi):

d/1.25	5	8	10	12	13	14	15
d	6.25	10	12.5	15	16.25	17.5	18.75
p	1350	850	680	560	530	490	450

Se rappresentiamo d e p con dei punti otteniamo:

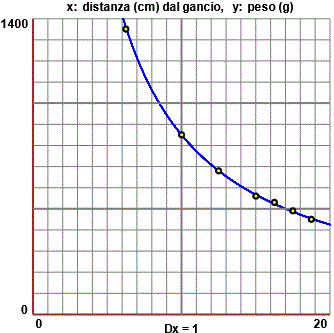
Vedo che posso approssimare l'andamento dei punti con una curva.  Seguendo l'indicazione del testo del quesito calcoliamo i prodotti d*p.  Per fare il calolo usiamo ad esempio lo script "operaz tra seq" presente qui, ma potremmo usare altri software:

x: 6.25, 10, 12.5, 15, 16.25, 17.5, 18.75  y: 1350,850,680,560,530,490,450  [x]
8437.5,8500,8500,8400,8612.5,8575,8437.5
somma = 59462.5
x:  59462.5  y: 7  [/]
8494.642857142857

Ho calcolato anche il valor medio dei prodotti d·p, arrotondando 8495. Nel grafico precedente la curva tracciata è proprio  p = 8495/d.  Il grafico è stato tracciato con questo script.

A destra una bilancia funzionante in modo simile (chiamata "stadera"); è un tipo di bilancia usato tuttora. Questo esemplare è stato trovato a Pompei (risale, quindi, al 79 a.C.).