|
Quante soluzioni reali ha la seguente equazione risolta rispetto ad X? |
|
(X6 + π)·(5X + 1)·(X + 2)2·(X3 – 1) = 0 |
|
(A) è una equazione di grado 12: non se ne conosce una formula risolutiva; quindi non si può rispondere al quesito
(B) 3
| |
(C) 12
(D) 4
(E) 6
|
|
(X6 + π)·(5X + 1)·(X + 2)2·(X3 – 1) = 0
quando 5X+1=0 o X+2=0 o X3-1=0 (X6+π non è mai 0).
Quindi -1/5, -2 e 1 sono gli unici numeri (reali) che sostituiti a x rendono l'equazione vera.
La risposta corretta è "3 soluzioni".
Le soluzioni le puoi trovare anche con WolframAlpha
introducendo:
solve (x^6+pi)*(5*x+1)*(x+2)^2*(x^3-1) = 0 for x real
Nota. Ogni eq. polinomiale di grado N ha al piugrave; N soluzioni, ma
non è vero che ogni eq. polinomiale di grado N ha N soluzioni!!! x100=0 è vera solo per x=0;
in alcuni ambiti matematici particolari, per affrontare alcune questioni
(ad es. precisare quanto in prossimità della soluzione la curva y=… si "spiaccica" sull'asse x), può essere
utile, negli ultimi anni delle scuole ad indirizzo scientifico, introdurre il concetto di molteplicità, e dire che, ad es. per questa equazione, 0 è una soluzione di molteplicità 100
(ribadiamo: sarebbe un'enorme sciocchezza, specie nell'insegnamento, dire che ha 100 soluzioni coincidenti: 100 ≠ 1!).
Per altro l'introduzione generalizzata del concetto di molteplicità per le soluzioni delle equazioni polinomiali nell'insegnamento preuniversitario
favorisce una rigida separazione tra i polinomi formali dell'algebra e quelli funzionali dell'analisi, seprazione tipica delle buffe e diffuse forme di insegnamento in cui si anticipa lo studio dei polinomi rispetto a quello delle funzioni.
Per altri commenti si veda la nota sulla "formula risolutiva delle eq. di 2° grado" alla voce  funzioni polinomiali deGli Oggetti Matematici.
funzioni polinomiali deGli Oggetti Matematici.
Si noti, inoltre, che la formulazione della risposta A non è
corretta: il teorema di Ruffini-Abel non afferma che per le equazioni polinomiali in x P(x)=0 di grado maggiore
a 4 non esistono formule od altri procedimenti risolutivi, bensì che non esistono formule generali
che consentano di esprimere le soluzioni (rispetto a x) come funzioni dei coefficienti
di P(x) ottenute componendo solo le quattro operazioni ed estrazioni di radice (quadrata o di ordine superiore)!
In un test sottoposto a una quarantina di laureati in facoltà scientifiche (nel 2000) il quesito ha avuto solo il 38% di risposte corrette.
Il 19% ha scelto "12 soluz.", il 16% "4 soluz.". Il 27% ha preferito non rispondere.
Vediamo anche la rappresentazione grafica.
Grafici con questo e poi (zoommando) questo semplici script
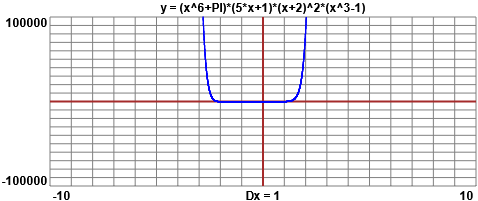
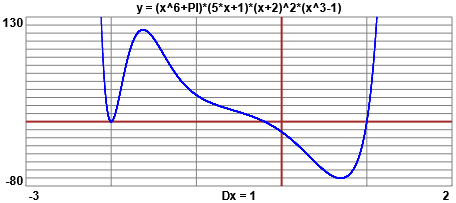
I grafici con WolframAlpha:
vedi qui
plot (x^6+PI)*(5*x+1)*(x+2)^2*(x^3-1)
plot (x^6+PI)*(5*x+1)*(x+2)^2*(x^3-1)=0 | |
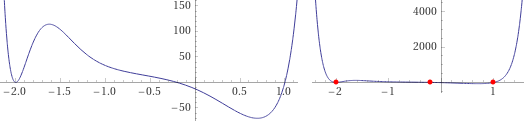 |
 funzioni polinomiali deGli Oggetti Matematici.
funzioni polinomiali deGli Oggetti Matematici.

