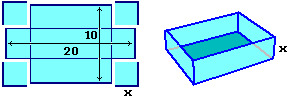
Voglio costruire una scatola tagliando da una lamiera rettangolare di dimensioni 20 cm × 10 cm quattro quadratini e operando successive piegature e saldature: vedi figura. Come devo effettuare il taglio affinché abbia volume di 100 cm3?
[Traccia: indica con x il lato in cm dei quadratini, esprimi con una formula il volume in cm3 V della scatola; usando la calcolatrice tabula e traccia il grafico di V in funzione di x; cerca in questo modo di individuare il lato con cui prendere i quadratini arrotondato ai millimetri]

Mi esprimo in cm.  V = AreaBase·Altezza = (20-2x)(10-2x)x Come dominio di V devo prendere i valori di x compresi tra 0 e 5 (non posso tagliare quadratini di lato maggiore di 5 in quanto una delle dimensioni della lamiera è 10). Tabulo V e traccio il grafico; traccio la retta orizzontale che corrisponde a V =100. Trovo facilmente che x deve valere circa 0.6 o 4.0. Sul fatto che 0.6 sia il valore troncato ai decimi che meglio approssima l'ascissa del punto di intersezione a sinistra non ho dubbi. Per quello a destra sono incerto tra 3.9 e 4.0. Per sciogliere il dubbio calcolo:   V(3.95) = 100.3695 Concludo che per x = 3.95 il grafico sta sopra a V = 100. Quindi l'ascissa dell'intersezione è maggiore di 3.95: prendo quindi 4.0 invece che 3.9. Per altri commenti: 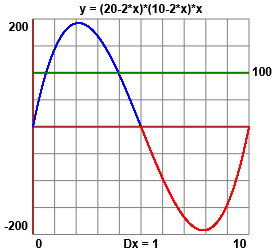risoluzione equazioni(2) neGli Oggetti Matematici

Come risolvere l'equazione (e tracciare il grafico) con WoframAlpha:

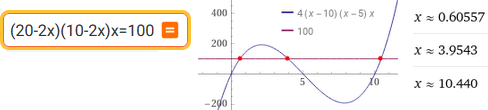
Come risolvere l'equazione col semplice script "equazioni", dopo aver sviluppato (20-2x)(10-2x)x in 4x³-60x²+200x:

Il grafico iniziale è stato realizzato con questo script.