Determina questi valori arrotondati ai decimi.
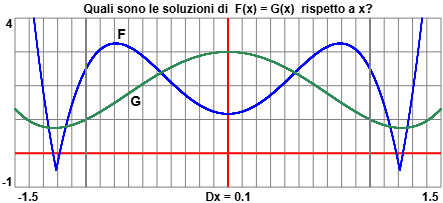
| L'equazione F(x) = G(x) è vera per sei valori di x appartenenti all'intervallo Determina questi valori arrotondati ai decimi. |  |
Dobbiamo individuare le tacche dei decimi più vicine alle ascisse dei punti di intersezione dei grafici di F e di G. Esse corrispondono ai valori 0.5, 1.1, 1.3 e ai loro opposti -0.5, -1.1 e -1.3.
È un esercizio che mira a mettere a fuoco il significato "grafico" della risoluzione delle equazioni. Questo è un aspetto in genere trascurato dall'insegnamento tradizionale, che tende ad affrontare la risoluzione delle equazioni in un contesto di pura manipolazione algebrica, senza sviluppare l'attenzione alla sua interpretazione geometrica, utile anche a controllare la sensatezza delle soluzioni eventualmente trovate, oltre ad eventualmente indirizzare verso delle strategie di risoluzione.
Lo script con cui è stato costruito il grafico.
La soluzione "esatta" (con WolframAlpha) utilizzando la descrizione algebrica dei grafici contenuta nello script precedente:
