Il primo termine è maggiore del secondo o viceversa, o sono uguali, o la cosa varia a seconda dei valori di R e T.  Motiva la risposta.

Proviamo subito con qualche esempio, con R e T "piccoli" e "grandi":
R = T = 1; ho 3+4 < (3+4)/2;
R = T = 2; ho (3+4)/2 = (3+4)·2/4 = (3+4)/2;
R = T = 4; ho (3+4)/4 > (3+4)·4/8 = (3+4)/2

Abbiamo trovato la risposta.

    Bisogna non farsi ingannare. In molti esercizi scolastici si propongono un mucchio di calcoli con formulette, semplificazioni, … che facilitano il procedimento. Ma, in realtà, cose del genere non accadono spesso (almeno nella matematica che si usa, diversa da quella dei libri di testo più commerciali).

    Senza fare ragionamenti più complicati vediamo di illustrare la sitazione esaminando il grafico della curva  3/R+4/T = (3T+4R)/(R+T), che proviamo a trasformare con qualche semplice manipolazione, tenendo conto che R e T sono positivi.

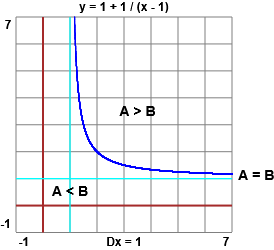
    Il grafico è l'iperbole R = 1/T alzata di 1 spostata a destra di 1.  Nella figura seguente y è R, x è T, A è 3/R+4/T, B è (3T+4R)/(R+T).  I punti che stanno sul grafico sono quelli in cui i due termini sono eguali, quelli a sotto e a sinistra quelli in cui il primo è minore del secondo, quelli sopra e a destra quelli in cui è maggiore. Sono evidenziati i punti corrispondenti agli esempi fatti sopra.

   Il grafico è stato fatto con questo script.  La relazione R = T/(T-1) potremmo studiarla anche con WolframAlpha introducendo
        solve 3/R+4/T = (3T+4R)/(R+T) for R, T > 0, R > 0