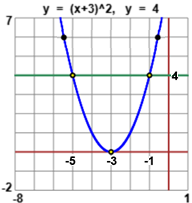
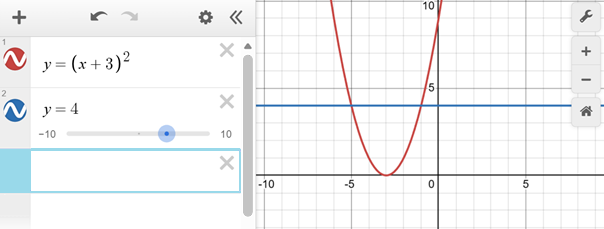
Dove si incontrano la curva  y = (x+3)²  (è una "parabola") e la retta  y = 4 ? (x+3)²  vale 0 quanto x = -3; per gli altri valori di x ha un valore maggiore di 0.  Quando vale 4?  Quando x = -1 o quando x = -5. Il grafico di  y = (x+3)²  potremmo tracciarlo con precisione calcolando quanto vale y per svariati valori di x. Potremmo trovare dove si incontrano la parabola e la retta senza tracciare il grafico?  Sì, risolvendo l'equazione  (x+3)² = 4. Vediamo come. Qual è un numero il cui quadrato è 4? Sicuramente 2:  2·2 = 4. Ma non solo:  anche (-2)·(-2) = 4.  In altre parole l'equazione (nell'incognita z) z² = 4 ha due soluzioni, z = 2 e z = -2. Quand'è che (x+3)² = 4?  Quando x+3 = 2 e quando x+3 = -2  (infatti √4 = 2).  Ovvero quando  x = 2-3 = -1  e quando  x = -2-3 = -5. Abbiamo ritrovato gli stessi valori che avevamo individuato procedendo graficamente. Quand'è che (x+3)² = 6?  Quando x+3 = √6 e quando x+3 = -√6, quindi quando x = √6-3 e quando x = -√6-3.  Con la calcolatrice troviamo i valori -0.55051025721... e -5.44948974278..., a cui corrispondono i pallini neri nel grafico.

Trova per quali valori di x  (x-2)² = 9  e per quali valori di z  (3+2z)² = 10.

(x-2)² = 9  →  x-2 = √9 = 3  oppure x-2 = -√9 = -3  →  x = 3+2 = 5 oppure x = -3+2 = -1.
Controlliamo:  per x = 5  (x-2)² = 3² = 9;  per x = -1  (x-2)² = (-3)² = 9.  OK

(3+2z)² = 10  →  3+2z = √10  oppure 3+2z = -√10  →  2z= √10-3 oppure 2z= -√10-3  →  z = (√10-3)/2 oppure z = (-√10-3)/2  →  z = 0.08113883008... oppure z = -3.08113883008...
Controlliamo (in modo approssimato):
per z = 0.08113883008  (3+2z)² = 9.999999999947;  per z = -3.08113883008  (3+2z)² = 9.999999999947.  OK

Qui sotto la figura realizzata con Desmos: vedi.