Un'industria produce due prodotti A e B e utilizza due macchinari P e Q. Per ogni kg di A sono necessarie 1 ora e mezza di P e 3 ore di Q, per ogni kg di B sono necessarie 2 ore di P e 2 ore e mezza di Q. Inoltre A non può essere prodotto in più di 17 kg alla settimana, la macchina P non può lavorare per più di 40 ore alla settimana, mentre Q per non più di 55.  Sia m l'unità di misura monetaria in vigore.  Determinare qual è la combinazione produttiva più conveniente, sapendo che ogni kg di A viene venduto a 15000 m e ogni kg di B a 9000 m, nell'ipotesi che ogni quantità prodotta sia venduta, e che i costi di produzione siano sostanzialmente indipendenti dalla scelta operata.

Schema risolutivo

	A	B	Ore  disponibili	x = quantità di A  y = quantità di B  z = funzione obiettivo = ricavo
P	1.5	2	40
Q	3	2.5	55

max	z = 15000 x + 9000 y
	1.5x + 2y ≤ 40
	3x + 2.5y ≤ 55
	x +  0y ≤ 17
	x +  0y ≥ 0
	0x +   y ≥ 0

Con WolframAlpha:
maximize[15000x+9000y, {1.5x+2y<=40 && 3x+2.5y<=55 && x<=17 && y>=0 && x>=0} ]

        269400 at (x, y) = (17, 1.6)

    Conviene produrre 17 kg di A e 1.6 kg di B.

    Ecco la rappresentazione (e la soluzione) grafica del problema:

Con WolframAlpha, regione e retta 15000 x + 9000 y = 0:
plot 15000x+9000y=0, 1.5x+2y=40, 3x+2.5y=55, x=17 , y=0 , x=0, -5 < x < 25, -5 < y < 25

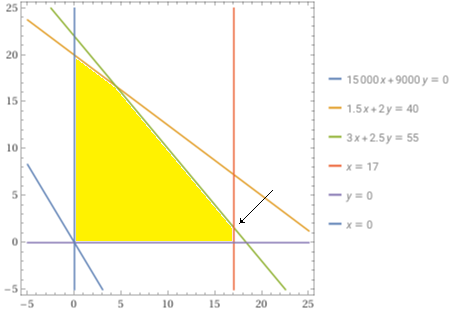
Approfondimenti in: Programmazione lineare neGli Oggetti Matematici.