Trova la funzione polinomiale, di grado più piccolo possibile, il cui grafico passi per esattamente i punti seguenti:  (−1, −10),  (0, −1),  (1, −2),  (2, 5). Prima di fare i calcoli prova a tracciare a mano il grafico. Trovata la funzione, tracciane il grafico usandone l'espressione, e confrontalo col precedente grafico.

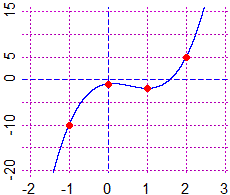
In questo esercizio si è visto che per 4 punti di ascisse diverse può passare una cubica, ossia il grafico di una funzione polinomiale di grado 3, o quello di una funzione polinomiale di grado più basso. Se tracciamo i punti e poi proviamo a tracciare a mano il grafico di essa, otteniamo una curva simile a quella raffigurata qui a destra. Troviamo, ora, la curva y = ax3+bx2+cx+d imponendo che passi per i quattro punti:         a·(-1)+b·1+c·(-1)+d = -10         a·0+b·0+c·0+d = -1         a·1+b·1+c·1+d = -2         a·8+b·4+c·2+d = 5 Risolviamo il sistema:

d = -1   (ex seconda equazione)
a + b + c = -1   (ex terza equazione)
-a + b - c = -9   (ex prima equazione)
8a + 4b + 2c = 6  ovvero  4a + 2b + c = 3  (quarta equazione)
b = -5   (ho sommato ex 3ª ed ex 1ª)
3a + 3b = -6  ovvero  a + b = -2  (ho sommato ex 1ª e 4ª)
a - 5 = -2  ovvero  a = 3
c = -1 - a - b = -1 -3 + 5  ovvero  c = 1

Quindi la curva è   y = 3x³ − 5x² + x − 1

    Con lo script "sistemi equazioni" (qui):

Nel caso di soli 4 punti potevo usare anche tecniche di regressione.