Dimostra che per N punti del piano cartesiano (N intero maggiore di 1) di ascisse tutte diverse tra loro passa il grafico di esattamente una funzione polinomiale di grado N−1 o più basso.

    Per capire la situazione partiamo da qualche N particolare.
Per N = 2 la cosa sicuramente funziona: per due punti di ascissa diversa passa esattamente una retta non verticale, che è dunque il grafico di una funzione polinomiale di grado 1 o, se è orizzontale, di grado 0 (in realtà, se i due punti stanno sull'asse orizzontale, potrebbe trattarsi delle funzione nulla, che, ad essere rigorosi, non possiamo considerare come una funzione di grado 0: funz. polinomiali).
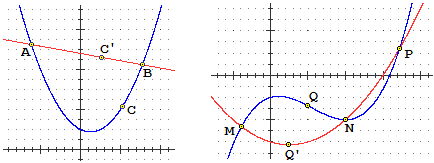
    Per N = 3 (figura sotto a sinistra) o abbiamo tre punti allineati, nel qual caso rientriamo nel caso precedente, o abbiamo tre punti per cui passa una parabola, la cui equazione può essere trovata imponendo che sia soddisfatta dalle coordinate dei tre punti:
  a x_A² + b x_A + c = y_A,  a x_B² + b x_B + c = y_B,  a x_C² + b x_C + c = y_C.

Si tratta, infatti, di un sistema lineare a 3 equazioni e 3 incognite (a, b e c) che sappiamo risolvere:  dalle prime due equazioni, che possiamo pensare nelle incognite b e c, ricaviamo i valori di b e di c pensando a come un parametro ( sistemi di equazioni).  Sostituitiamo questi valori nella terza equazione, che, a questo punto, possiamo pensare cone equazione di primo grado nella sola incognita a, e ricaviamo il valore di a.  Sostituiamo questo valore nelle due equazioni precedenti ed abbiamo anche i valori di b e di c.  Ma potremmo svolgere il calcolo anche in modi diversi.  Facciamo un esempio.  Se A = (-2,3), B = (3,2) e C = (1,1) ho:
(-2)²a - 2b + c = 3,  3²a + 3b + c = 2,  a + b + c = 1, ossia:
4a - 2b + c = 3,  9a + 3b + c = 2,  a + b + c = 1, da cui:
b = -1/5 - a,  c = 13/5 - 6a,  e quindi  -1/5 - a + 13/5 - 6a = 1, da cui:
a = 7/30, b = -13/30, c = 6/5.

    Con lo script "sistemi equazioni" (qui):

    Per N = 4 (figura in alto a destra) o abbiamo 4 punti allineati, nel qual caso rientriamo nel primo caso, o abbiamo 4 punti che stanno su una parabola, nel qual caso rientriamo nel caso precedente, o abbiamo quattro punti per cui passa una cubica, la cui equazione può essere trovata imponendo che sia soddisfatta dalle coordinate dei quattro punti.  Otteniamo un sistema lineare a 4 equazioni e 4 incognite (a, b, c e d) che risolviamo generalizzando la tecnica vista sopra: da tre equazioni troviamo a, b e c, pensando d come parametro. La quarta equazione diventa a questo punto ha la sola incognita d. La risolviamo e poi, sostitueindone il valore nelle altre equazioni, troviamo i valori delle altre incognite.
    Il procedimento, in modo analogo, si generalizza per qualunque N intero maggiore di 4 (con R possiamo usare xy_2, …, xy_7).

    Il procedimento lascia capire come risolvere, in generale, sistemi di equazioni lineari (formati N equazioni in N incognite). Per chi è interessato, il problema è discusso più in generale alla voce matrici.