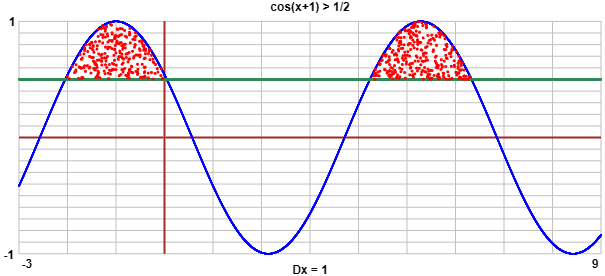
Risolvi rispetto a x la disequazione cos(x+1) > 1/2

cos(x+1) > 1/2 quando (si pensi al cerchio x²+y²=1) x+1 è compreso strettamente tra -60° (-π/3) e 60° (π/3) e quando sta in tutti gli intervalli ottenuti da questo aggiungendo/togliendo giri, ossia la disequazione è vera per ogni x tale che esiste un intero k per cui -π/3+2kπ < x+1 < π/3+2kπ, ossia -π/3-1+2kπ < x < π/3-1+2kπ. Possiamo valutare numericamente gli estremi degli intervalli: -π/3-1 = -2.04719…, π/3-1 = 0.04719….

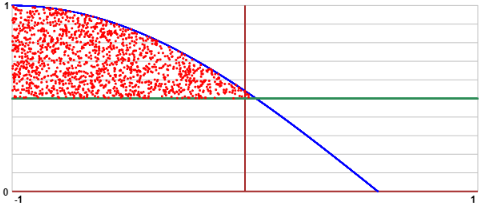
Posso controllare la soluzione ragionando sui grafici di x → cos(x+1) (grafico di cos traslato a sinistra di 1) e di x → 1/2: vedi figura sottostante. Si noti che il solo tracciamento dei grafici potrebbe ingannare: si potrebbe pensare che essi si incontrino in un punto di ascissa 0 invece che 0.04719…. Con uno zoom (se si fosse fatto il grafico col computer) si vedrebbe che i due grafici non si incontrano sull'asse y.

Per altri commenti:  funz. circolari e trigonometria neGli Oggetti Matematici.

Il grafico soprastante è stato realizzato con questo script

Posso procedere anche con WolframAlpha: plot cos(x+1) > 1/2 for x in [-3 ,9] solve cos(x+1) > 1/2 for x 1/3 (6 π n - π - 3)<x<1/3 (6 π n + π - 3) and n element of Z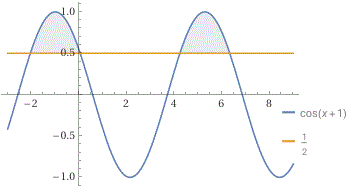