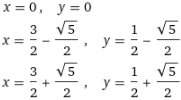Trova tutte le coppie di numeri tali che la loro somma, il loro prodotto e la differenza dei loro quadrati siano eguali.

Indichiamo con x ed y i due numeri. Dobbiamo avere  x+y = x·y = x²−y². Ovviamente la coppia x=0, y=0 soddisfa banalmente le condizioni. Vediamo se ci sono altre soluzioni.     Osserviamo subito che  x²−y² = (x−y)(x+y). 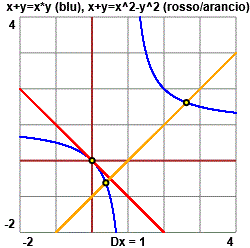Ci conviene quindi riscrivere le due eguaglianze così: x+y = x·y AND x+y = (x−y)(x+y)  ovvero: x+y = x·y AND (x+y = 0 OR 1 = x−y) y(1-x) = -x AND (y = -x OR y = x−1) y = x/(x-1) AND (y = -x OR y = x−1) y = 1+1/(x-1) AND (y = -x OR y = x−1) [↑ vedi figura a destra: intersezione tra iperbole e incrocio tra due rette] (y = 1+1/(x-1) AND y = -x) OR (y = 1+1/(x-1) AND y = x−1)     Le soluzioni sono sia il punto di intersezione tra la retta y = -x e l'iperbole y = 1+1/(x-1), sia i due punti di intersezione dell'iperbole con la retta y = x-1.     Il primo punto è x = 0, y = 0 (abbiamo ritrovato la soluzione trovata all'inizio). Le x degli altri due le trovo risolvendo x−1 = 1+1/(x−1), ossia (x−1)² = x, ossia x²−3x+1 = 0, da cui le soluzioni: x = (3+√5)/2, e y = (3+√5)/2−1, x = (3−√5)/2, e y = (3−√5)/2−1.     Verifico che questi valori − (3+sqrt(5))/2=2.618034, (3-sqrt(5))/2 = 0.381966 − corrispondono alle ascisse delle intersezioni delle due curve.

Posso controllare rapidamente la risposta con WolframAlpha: x+y = x*y = x^2 - y^2