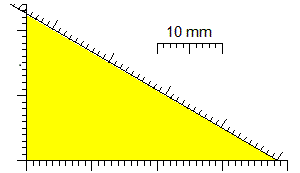
(1)  Verifica sperimentalmente il "teorema di Pitagora" nel caso illustrato a lato. (2)  In quale o quali contesti didattici potrebbe aver senso una tale "verifica", e una riflessione su di essa?

(1) Supponiamo che il triangolo sia esattamente rettangolo. Un cateto è lungo tra 22 e 23 mm; l'altro è lungo tra 38 e 39 mm; l'ipotenusa è lunga tra 44 e 45 mm. La somma dei quadrati dei cateti (espressa in mm2) cade tra 222+382 = 1928 e 232+392 = 2050. Il quadrato dell'ipotenusa cade tra 442 = 1936 e 452 = 2025. Gli intervalli [1928, 2050] e [1936, 2025] hanno intersezione non vuota (hanno l'intervallo [1936, 2025] in comune). Quindi il nostro rilevamento non è "in disaccordo" col teorema di Pitagora.

(2) Si tratta di una attività di calcolo approssimato che potrebbe essere svolta in vari contesti didattici.  Ad esempio nell'ambito di una attività di avvio al laboratorio di fisica, effettuabile in classe.  O nell'ambito di una riflessione più generale sul significato della verifica sperimentale di una legge fisica o di una formula riferita ad altri ambiti disciplinari, o sull'uso del simbolo "=" per indicare valori arrotondati:  si tratta di casi in cui le eguaglianze devono essere intese in senso approssimato.  Oppure potrebbe essere spunto per una riflessione sulla natura dei modelli matematici e, in particolare, della definizione matematica di spazio.  Vedi le voci Approximations e Space  qui.  Vedi anche gli esercizi 3.17 (sul calcolo approssimato) e 3.25 (sul teorema di Pitagora).  Vedi anche queste considerazioni sui triangoli, sul concetto di distanza, su numeri e approssimazioni.

Per i calcoli possiamo utilizzare anche il semplicissimo script "calcolo approssimato" presente qui:

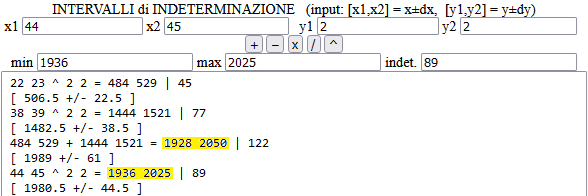
Altrimenti si può usare online www.wolframalpha.com. Vedi qui
minmax x^2+y^2 where abs(x-22.5)<0.5 and abs(y-38.5)<0.5
1928 at (x, y) = (22, 38)     2050 at (x, y) = (23, 39)
minmax x^2 where abs(x-44.5)<0.5
1936 at x = 44     2025 at x=45.