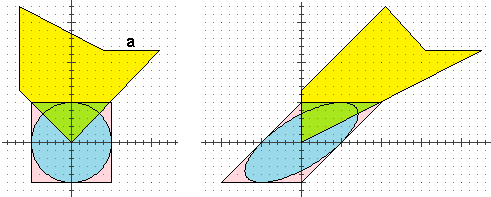Prova a solgere il seguente esercizio.  Poi affronta la domanda successiva.

A lato sono riprodotte, "incollate" su carta millimetrata, una figura, a sinistra, realizzata con Paint (o un'altra applicazione grafica) e l'esito di due sue successive trasformazioni, realizzate sempre con la stessa applicazione. (1) Quali comandi (e con quali parametri) sono stati utilizzati? (2) Queste trasformazioni potrebbero essere realizzate con due successive proiezioni da un piano ad un altro. Specifica per ciascuna se si tratta di una proiezione centrale o parallela, e come sono collocati piano di partenza, piano d'arrivo e raggi proiettanti.

L'esercizio ti suggerisce (direttamente o indirettamente) qualche considerazione didattica sui collegamenti tra l'insegnamento della geometria piana e quello della geometria tridimensionale?

L'esercizio

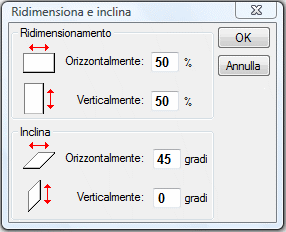
(1) Prima un "ridimensionamento" poi un "inclinamento", con i parametri riprodotti nella figura a lato. (2a) La prima trasformazione (una riduzione di scala monometrica, con fattore di scala 1/2), è realizzabile proiettando centralmente la figura con piano di arrivo parallelo al piano di partenza ed equidistante da questo e dal centro di proiezione (vedi figura A sotto a sinistra; nel caso B la riduzione di scala verrebbe composta con una rotazione di 180°; si otterrebbe la stessa figura, a meno di una isometria).
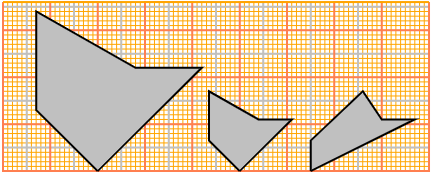
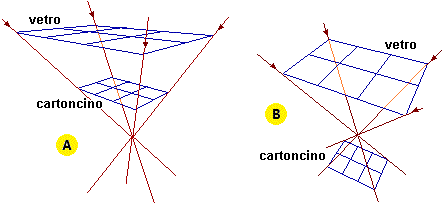
(2b) La seconda trasformazione è realizzabile mediante una opportuna proiezione parallela da un piano su un altro piano opportunamente inclinato. Per capire meglio la disposizione complessiva può essere utile provare a trasformare nello stesso modo una figura più articolata, come la seguente, e pensarla come ombra della figura originale disegnata su un vetro. 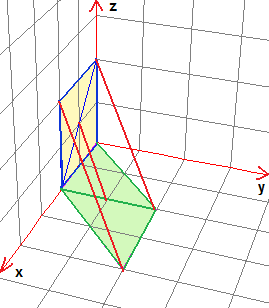Ci si convince facilmene che la si può ottenere, ad esempio, se la luce arriva come illustrato nella figura qui a destra. Non sarebbe facile descrivere questa disposizione a parole (senza ricorrere al sistema di riferimento xyz [lato a sull'asse x, piano di partenza: y=0, piano di arrivo: z=0, direzione proiezione: vettore (1,1,-1)] e/o a un sistema di riferimento polare). Proviamo (ma, certamente, non si tratterà di una descrizione agevolmente comprensibile):  il piano di arrivo è perpendicolare al piano di partenza e lo interseca in una retta parallela al lato a della figura originale; la proiezione ha direzione parallela ai piani perpendicolari al piano di arrivo e inclinati di 45° rispetto al piano di partenza e ai piani inclinati di 45° rispetto sia al piano di arrivo che a quello di partenza.

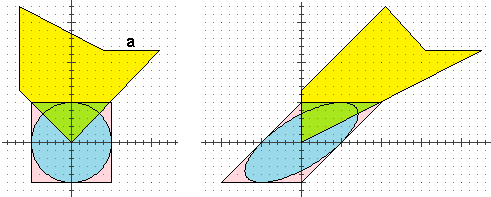Possibili considerazioni didattiche

• l'importanza di affrontare anche lo studio della geometria tridimensionale, impostato, come nel caso piano, non limitandosi allo studio di "figure" ma affrontando lo sudio dello "spazio" (sistemi di riferimento, coordinate, direzioni, ...),
• l'opportunità di affrontare, intreccandosi anche ad altre discipline (scienze-geografia, arte/disegno-prospettiva, fisica-ottica),
• la problematica della rappresentazione piana di figure tridimensionali,
• la motivazione dello studio delle trasformazioni geometriche piane (e delle coniche) attraverso la loro interpretazione 3D,
• la modellizzazione di problemi spaziali e la loro riconduzione a problemi di geometria piana,
• ...

Qualche link:  sull'importanza di affrontare lo studio di situazioni tridimensionali sin dalla scuola di base vedi il quesito 1a.22 e tutti gli altri esercizi richiamati nelle risposta;  per l'avvio alla formalizzazione delle questioni prospettiche vedi il quesito 2.51;  sulla questione dei rapporti con le arti figurative vedi il quesito 3.43 e i link a cui si viene rinviati nella risposta;  sulle rappresentazioni cartografiche e sulla (nostra) difficoltà a modellizzare i problemi spaziali vedi questo link (vai avanti visualizzando almeno una dozzina di immagini).