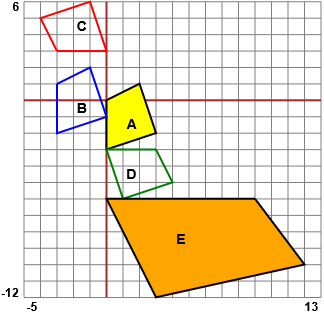
Come possono essere introdotte le trasformazioni affini a scuola (nelle medie inferiori e nelle superiori)? Prova, prima, a risolvere il seguente esercizio. La figura A subisce successive trasformazioni, scelte tra rotazioni attorno a generici punti, traslazioni, trasformazioni di scala, simmetrie centrali, simmetrie assiali, fino a diventare la figura E. (1) Individuare le successive trasformazioni, specificandone i parametri (ad es. per una traslazione indicarne i passi, per una rotazione indicarne centro e ampiezza, per una simmetria assiale indicarne l'asse). (2) La trasformazione complessiva è affine? (3) Che rapporto c'è tra l'area di E e quella di A?

Vediamo prima la soluzione dell'esercizio.

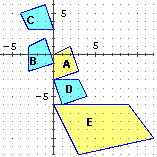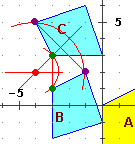
(1) • A→B: traslazione; (0,0) viene trasformato in (-3,1): questo è il vettore che rappresenta la traslazione, ovvero la traslazione ha passi Δx = -3, Δy = 1. • B→C: rotazione ampia 90° (si veda ad es. come cambiano le pendenze dei lati che comprendono l'angolo retto). Per individuare il centro di rotazione posso (vedi fig. a destra) fare l'intersezione degli assi delle corde corrispondenti agli archi di cerchio che descrivono le rotazioni di due qualunque vertici di B; trovo che il centro è (-4,2) • C→D: rotazione di 180° attorno a (0,0) o simmetria di centro (0,0). • D→E: trasformazione di scala (x,y) → (3x,2y).

(2) A→E è una trasformazione affine; la cosa può essere giustificata in vari modi, a seconda di come si definiscono le trasformazioni affini.
• Se definisco le trasformazioni affini come composizioni di isometrie e trasformazioni di scala, mi basta osservare che tutte le trasformazioni precedenti rientrano in queste categorie.
• Se definisco le trasformazioni affini algebricamente, come trasformazioni del tipo:
/x'\ = /a b\ × /x\ + /h\   con |a b| ≠ 0
\y'/   \c d/   \y/   \k/       |c d|
posso osservare che tutte le trasformazioni precedenti sono esprimibili così e sono quindi affinità e quindi lo è la loro composizione, dato che le affinità formano un gruppo.
• Se le definisco come trasformazioni del tipo:
/x'\   /a b h\   /x\     |a b h|
|y'| = |c d k| × |y| con |c d k| ≠ 0
\1 /   \0 0 1/   \1/     |0 0 1|
posso verificare che tutte le trasformazioni precedenti rientrano in questa categoria e, quindi, anche la trasformazione loro composta, che è rappresentata dalla matrice prodotto delle loro matrici, che risulta essere anch'essa di questa forma e con determinante diverso da 0.

(3) A→B, B→C, C→D sono isometrie, quindi conservano le aree; D→E moltiplica le aree per 3·2. Dunque il rapporto tra l'area di E e quella di A è 6.

Come possono essere introdotte le trasformazioni affini a scuola?

Il quesito apre una riflessione sulla problematica di come riprendere "a spirale" gli argomenti passando da un livello scolastico al successivo.  Nel nostro caso, ad es., si potrebbe ritenere opportuno avviare (nella scuola di base) alle affinità come ombre del sole e, poi, più in generale, come proiezioni parallele, individuando (attraverso attività dal vivo di collegamento di oggetti ad ombre, di esame dinamico di situazioni - cambiare posizione dell'oggetto o dello schermo -, ...) le proprietà mantenute dalle immagini, ... senza porsi il problema della loro rappresentazione analitica, che invece potrà essere avviata per alcune particolari trasformazioni affini (le traslazioni, le trasformazioni di scala, ed eventualmente le simmetrie rispetto agli assi).  Nelle superiori ci si potrebbe porre il problema di trovare il collegamento tra le trasformazioni affini intese come frutto di composizione di rotazioni, traslazioni, simmetrie e trasformazioni di scala (delle quali si può dare una interpretazione analitica) e le proiezioni parallele; una delle motivazioni potrebbe essere anche quella della esplorazione della modello analitico incorporato nei programmi di grafica.  Sicuramente secondaria, e da motivare (come? ... pensarci), e non da affrontare in tutte le scuole, è l'introduzione di una rappresentazione algebrica più generale delle trasformazioni affini.

Come è stata realizzata la figura?  VEDI