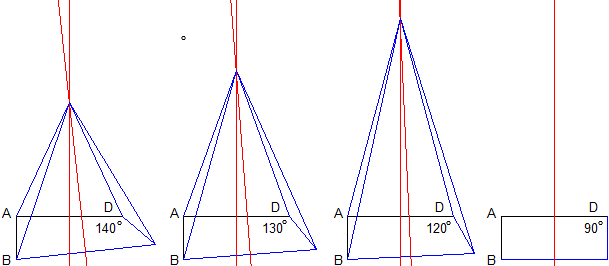
Considera la seguente dimostrazione di un fatto evidentemente falso (perché?). La figura è uno schizzo, impiegato per aiutare la comprensione della dimostrazione. Trova dove è l'errore. E rifletti sulle difficoltà e sul ruolo delle dimostrazioni nell'insegnamento.
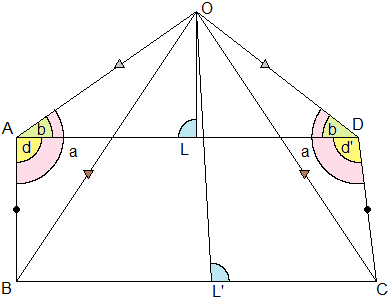
Teorema. Sia ABCD un quadrilatero con i lati AB e CD eguali e ∠BAD (indicato con d in figura) retto. Allora ∠ADC (indicato con d') è retto. Dimostrazione. (1) Siano L l'asse di AD, L' quello di BC e O la loro intersezione.  Dunque AO=OD, BO=OC. (2) Ma AB=CD. Quindi ABO e DOC sono triangoli uguali (o, meglio, inversamente eguali, o simmetrici). (3) Quindi ∠BAO=∠ODC (angoli indicati con a). (4) Essendo OAD isoscele, ∠DAO=∠ODA (angoli indicati con b). (5) Quindi (essendo differenze di angoli eguali) d e d' sono eguali.

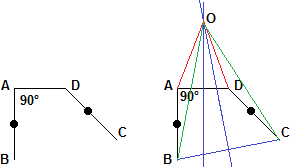La figura soprastante evidenzia che il teorema è falso. La proprietà è verificata solo se CD è parallelo ad AB.  Le figure seguenti illustrano meglio la situazione.  Il fatto è che il segmento OC non interseca il segmento AD come appare invece nel disegno che è stato schizzato.  Questo esemplifica una delle tipiche difficoltà delle dimostrazioni geometriche (spesso scavalcate nei libri di testo, in cui le dimostrazioni - a volte incomplete - sono riferite a figure la cui costruzione potrebbe essere giustificata solo dopo aver risolto la questione proposta dall'esercizio).  Non è facile, se non si ragiona "liberamente", risolvere questo esercizio.
L'esercizio mette in luce anche come è utile ricorrere al computer per studiare dinamicamente figure dipendenti da parametri.  Le dimostrazioni, in matematica, anche dei fatti più "evidenti", sono molto spesso articolate e lontane dal contesto a cui il "fatto" si riferisce (e ottenute dopo anni di tentativi da parte di più persone);  in alcuni casi sono affrontabili solo con complessi calcoli gestibili unicamente mediante il computer.  Per altro il nostro cervello non è adatto ai lunghi ragionamenti rigorosi necessari per comprendere le dimostrazioni matematiche.  Questa (accanto a motivazioni culturali presenti nel documento a cui si viene rinviati sotto) è una delle ragioni per cui le dimostrazioni non devono essere uno strumento per costruire le conoscenze matematiche ma un oggetto di conoscenza.
Il ricorso al computer e la possibilità con esso di intrecciare ragionamenti sintetici e analitici (e di studiare le figure dinamicamente) consente di affontare in modo più amichevole e comprensibile (anche non dai cosidetti "geni") i problemi e le argomentazioni geometriche.

L'esempio è tratto dal libro di Stanislas Dehaene "La Bosse des maths" (Paris, Odile Jacob, 1997), tradotto in italiano come "Il pallino della matematica" (Mondadori, 2000).