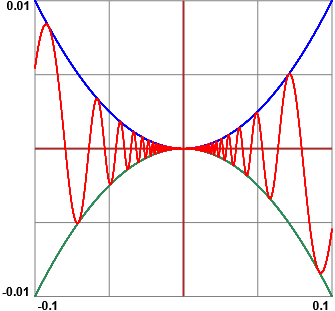In un libro di testo si introduce intuitivamente il concetto di funzione derivabile in x₀ come quello di una funzione il cui grafico zoommato sempre più attorno al punto di ascissa x₀ tende ad assomigliare sempre più ad una retta. Analizza aspetti positivi e negativi di un tale approccio.

Questo è un tipico esempio in cui il modo in cui ci si esprime per introdurre intuitivamente un concetto può essere portatore di misconcezioni che poi è difficile smontare:  è corretto (e sensato) avviare al concetto di derivata in k di F come pendenza a cui tende la retta passante per il punto del grafico di F di ascissa k e un altro punto di ascissa x man mano che x si avvicina a k, ma non è vero  (se F non ha la derivata prima continua)  che il grafico di F tenda a diventare una retta.  Vedi l'esempio sottostante e queste immagini.

F(0) = 0, F(x) = sin(1/x)·x2 se x ≠ 0

Per quanto zoommi il grafico di F attorno a 0 continua ad oscillare, ma in 0 F è derivabile: F'(0) = 0
La spiegazione del libro favorisce il formarsi dell'idea che in casi come questo la derivata non esista.