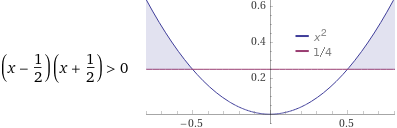
Quali tipi di
difficoltà mediamente può trovare uno studente di fine superiori (in
Italia ai nostri giorni) di fronte alla risoluzione di una
disequazione come
Di fronte a x2 > 1/4 ci si aspetta che molti studenti rispondano x > ±1/2, per analogia
con la risoluzione di x2 = 1/4. Ci si aspetta anche che, tra coloro che capiscono quale sia la soluzione, molti la esprimano
in modo errato, ad esempio con
Anche tra coloro che rispondono correttamente, ci aspettiamo che non pochi usino formule e tecniche di manipolazione generali
per risolvere disequazioni del tipo
All'origine di queste difficoltà vi è la tendenza, da parte degli alunni, ad applicare procedimenti risolutivi appresi solo meccanicamente:
perso l'allenamento a risolvere esercizi di un certo tipo, non riescono a ricordarne i corripondenti metodi risolutivi o non sono più in grado ad associare procedimenti
a problemi corrispondenti. Questa tendenza è favorita da un insegnamento che articola la matematica in tanti temi e attività separate, e che in particolare non mette a fuoco le poche idee generali che servono per risolvere tutti i tipi di disequazioni (assieme alle caratteristiche delle particolari funzioni via via coinvolte) e che non intreccia
metodi simbolici e metodi grafici (idee generali e intreccio che, a differenza delle singole procedure risolutive, gli alunni avrebbero occasione di rivedere, consolidare, applicare, … nel corso di tutto il quinquennio).

La presenza di difficoltà di questo tipo sono state evidenziate da un'indagine sulle competenze degli alunni dell'ultimo anno delle superiori. Vedi il seguente quesito e i commenti.
| Se x è un numero reale tale che x2 > 9, allora: | ||||
| (1) | x < –3 o x > 3 | (3) | x < ± 3 | |
| (2) | x < –3 e x > 3 | (4) | x > ± 3 | |
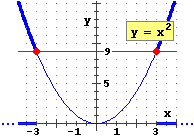 |
Se un punto del grafico di y = x2 sta sopra alla retta y = 9 la sua ascissa deve essere minore di -3 o maggiore di 3 (vedi figura): x < –3 o x > 3 La risposta (4) (che non potrebbe venire in mente se si pensasse ai grafici) non ha molto senso di per sé: la condizione x > -3 include la condizione x > 3. La risposta (2) confonde "e" con "o". La confusione è favorita dal fatto che talvolta si usa "e" per indicare l'unione tra due insiemi (sarebbe corretto dire: sono soluzioni della disequazione i numeri x tali che x < –3 e quelli tali che x > 3, ma … questi sono i numeri x tali che "x < –3 o x > 3"). A scuola (e nelle soluzioni indicate dai libri) a volte "e", "o" e "," sono usati in modo errato; ad esempio viene scritta "x<–3, x>3" come soluzione, invece di "x<–3 o x>3" o, ad es., |
In un test sottoposto (nel 2004/05) a 1394 studenti dell'ultimo anno delle superiori solo il 24% ha risposto correttamente, il 45% ha scelto (2) e ben il 27% ha scelto (4).