Spiega, eventualmente con qualche esempio, come l'interpretazione geometrica ("mentale" o con uno schizzo) di una equazione può, spesso, essere di aiuto per la risoluzione "esatta" di una equazione.

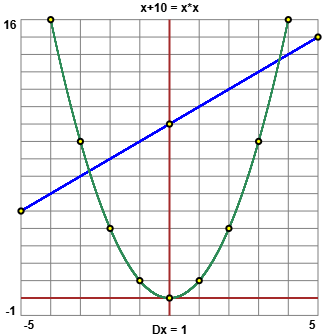
• Di fronte all'equazione  x² - x - 10 = 0  posso immaginare i grafici di y = x² (parabola) e di y = x+10 (retta) e capire che ci sono due soluzioni, una positiva ed una negativa. Posso schizzare a mano i grafici e capire che le soluzioni sono tra -3 e -2 e tra 3 e 4. Sotto a sinistra i grafici fatti col computer (vedi). Posso poi (se ho già imparato a risolvere le equazioni di 2º grado) risolvere l'equazione e controllare i valori ottenuti con quanto dedotto dalla rappresentazione grafica.

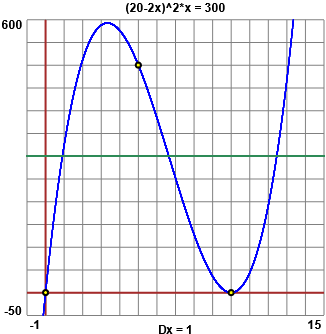
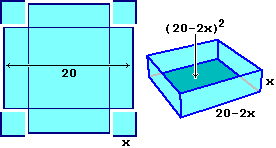• Devo realizzare una scatola del volume di 300 cm³ tagliando da una lamiera quadrata di lato 20 cm quattro quadratini di lato x cm e operando successive piegature e saldature. Come devo effettuare i tagli?  Devo trovare le soluzioni tra 0 e 10 di (20–2x)·2x = 300. Schizzando i grafici (sopra realizzati con questo script) capisco che ci sono due soluzioni, una vicina ad 1 (cm), l'altra vicina a 7. Facendo il grafico col computer in scale diverse posso trovare con la precisione che voglio le soluzione. Se conosco tecniche per risolvere algebricamente le equazioni polinomiali di 3º grado posso trovare le soluzioni esatte; altrimenti posso ricorrere a questo script o ad un programmino in JavaScript (vedi) o a WolframAlpha.

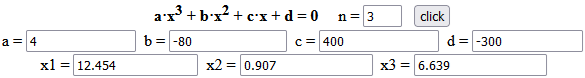Prendo le soluzioni tra 0 e 10 0.907 (o 0.91) cm, 6.639 (o 6.64) cm

• Di fronte all'equazione  sin(x) = -0.7  prima di mettermi a fare calcoli schizzo il grafico della funzione sin e quelo di y = -0.7 per capire approssimativamente quali sono le soluzioni (sotto il grafico fatto con questo script). Capisco che sono circa 4 e 5.5 e tutti i numeri ottenuti da questi aggiungendo o togliendo multipli di 2π.

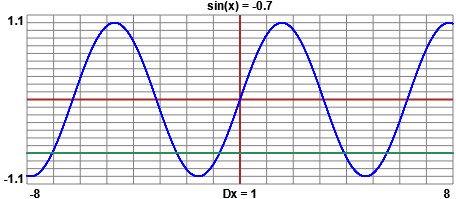Posso fare poi i calcoli con una calcolatrice (ad es. questa):   asin(-0.7) = -0.775397496610753,
-0.775397496610753 + (2*PI) = 5.507787810568833,
-0.775397496610753 + (3*PI/2) = 3.936991483773937
O posso impiegare WolframAlpha.

Due ultimi esempi.

• Di fronte all'equazione x³-2x-q = 0 con incognita x e parametro q per capire come varia la quantità delle soluzioni al variare di q posso tracciare y = x³ e un po' di rette y = 2x+q. Vedi il grafico sottostante a sinistra (ottenuto con questo script).

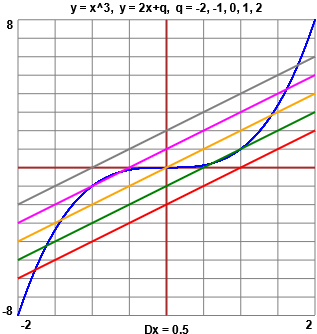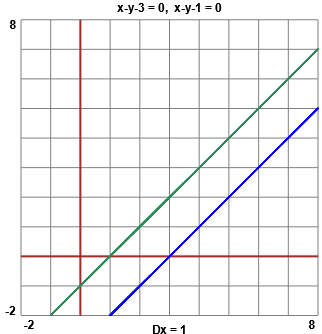• Di fronte al sistema  y-x-3 = 0 & y - x - 1 = 0  posso tracciare i grafici delle due rette (rappresentazione grafica sopra a destra, ottenuto con questo script) per mettere a fuoco (e rafforzare la comprensione) che non ci sono soluzioni.