Verificate, con l'aiuto del computer, nel modo che ritenete più opportuno, che per n intero positivo
Questo è un esempio di esercizio che può essere rivolto all'intera classe, eventualmente organizzata a gruppi, in cui possono emergere, e confrontarsi, diverse strategie e tecniche. Qui vedremo alcune dei possibili modi in cui affrontare la questione e, poi, accenneremo a come "dimostrare" la proprietà.
• Potremmo affrontare il calcolo con un programmino. Vediamo come farlo con JavaScript.
function F(n) { return Math.pow(n*(n+1)/2,2) }
function G(n) { S=0; for(i=1;i<=n;i=i+1) {S=S+i*i*i}; return S}
N=30; for(j=1;j<=N;j=j+1) document.write(j," ",F(j)," ",G(j),"<br>")
uscite:
1 1 1
2 9 9
3 36 36
4 100 100
5 225 225
...
29 189225 189225
30 216225 216225
• Potremmo affrontarlo utilizzando qualche software che consenta di operare su sequenze. Ad esempio impiegando questo script (presente come "operaz tra seq" fra questi):
x 1,2,3,4,5,6,7,8,9,10 y 3,3,3,3,3,3,3,3,3,3 ^ 1,8,27,64,125,216,343,512,729,1000 somma somma = 3025 x 5 y 11 × 55 x 55 y 2 ^ 3025
• Vi sono anche calcolatrici che consentono di effettuare calcoli di questo genere; ad esempio questa. Vedi.
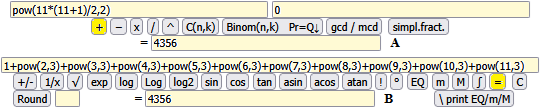
• Un modo molto semplice è usare una calcolatrice, ad es. la calcolatrice online "calcolatrice2" presente qui, nella quale xy si indica

Con la stessa calcolatrice potevo impiegare il tasto [N] per generare sequenze qualunque di numeri naturali e poi i tasti [data^Q] (Q = 3) e [sum]. Ad esempio nel caso dei primi 11 termini metto 11 e premo [N]; poi metto 3 in Q e premo [data^Q], in modo da ottenere da ottenere i primi 11 interi positivi elevati alla terza; poi copio questa sequenza di numeri sopra a [N] e premo [sum] ottenendone la somma:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 Q = 3 data^Q: 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331 sum = 4356
• Volendo si può impiegare anche un foglio di calcolo.
• Col sofware online WolframAlpha basta introdurre 1^3+2^3+3^3+...+n^3 per ottenere

• Si può poi accennare agli alunni che questa proprietà, di cui, come abbiamo visto, è facile convincersi della validità, può essere dimostrata, e si può, in alcune classi, esaminare la dimostrazione:
