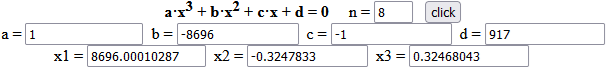
Un insegnante decide di proporre agli studenti (in una classe seconda di scuola superiore) la risoluzione dell'equazione:
x³ − 8696·x² − x + 917 = 0
L'idea è quella di far loro usare del software per ricercare le soluzioni con metodi grafici e/o numerici (comprensibili), senza l'impiego di WolframAlpha che la risolverebbe automaticamente. Secondo te, quali problemi vorrebbe far emergere e/o quali questioni vorrebbe affrontare/sistemare l'insegnante con questa attività?

Vediamo, innanzi tutto, a livello adulto, come si potrebbero trovare le soluzioni.
(1)  Un primo modo è quello che tiene conto che si tratta di una equazione polinomiale. Potremmo usare uno dei molti software che cosentono di risolvere equazioni di questo tipo.

a)  Un primo metodo è ricorrere ad uno script per risolvere numericamente vari tipi di equazioni equazioni (questo - col nome "equazioni" e altri script puoi trovarli qui):

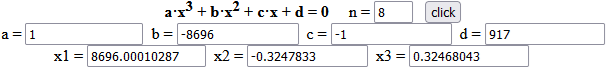
b)  Usando WolframAlpha avrei ottenuto direttamente:

x^3-8696*x^2-x+917 = 0
                      
x ≅ -0.324783298321785
x ≅ 0.324680429277547
x ≅ 8696.00010286904

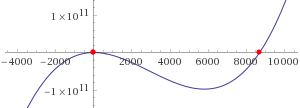
(2)  In alternativa posso trovare le soluzioni con un programma per tracciare i grafici. Vediamo, ad esempio, come ricorrere a questo script.

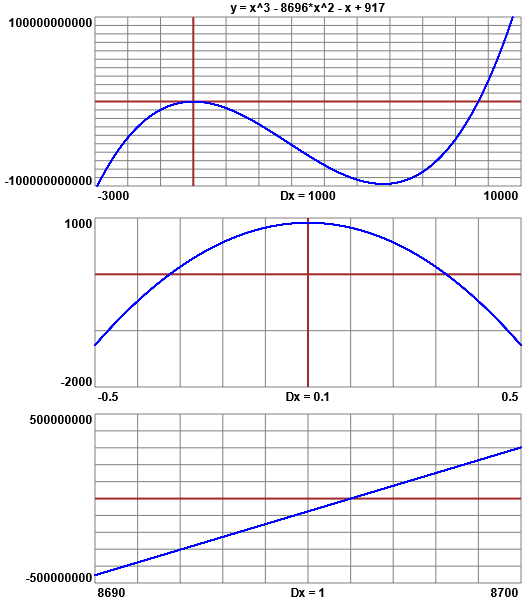
Se mi fermo qui, e non faccio ulteriori zoom, posso concludere che le soluzioni, approssimate, sono:  -0.32,  0.32,  8696.
Ma potrei fare ulteriori zoom.

(3)  Posso trovare le soluzioni con un semplice programmino per risolvere le equazioni F(x)=0 in un intervallo in cui F cambi segno, dopo essermi fatto un'idea dell'andamento del grafico o procedendo direttamente per tentativi (tenendo conto che si tratta di una equazione cubica, con da 1 a 3 soluzioni). Il programmino può essere questo in JavaScript:

function F(x) {return Math.pow(x,3)-8696*x*x-x+917 }
a=-1000; b=0
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
       m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
       if(y1*y2 > 0) {a = m} else {b = m} }
    document.write(m)
}

Output:  -0.3247832983217851

a=-1; b=1000  ->  0.3246804292775467

a=1000; b=10000  ->  8696.000102869042

Quali potrebbero essere gli obiettivi di chi propone questo problema − da affrontare con gli strumenti descritti in (2) o (3) o in (1a) − agli alunni di una classe seconda di una scuola superiore?

•  far riflettere gli alunni, mettendoli in crisi, sul fatto che senza qualche ragionamento il solo uso del computer non consente di trovare con certezza tutte le soluzioni: anche facendoli lavorare a gruppi probabilmente (se non viene introdotto lo script (1a) [o se viene proposta un'equazione di grado 5 non affrontabile con quello script]) vengono individuate solo le due soluzioni tra −1 ed 1;
•  avviare considerazioni sulle equazioni polinomiali, che conducano alla messa a fuoco del teorema del resto e della sua conseguenza che una equazione polinomiale in una incognita ha al pi tante soluzioni quanto è il suo grado;
•  mettere a fuoco il fatto che l'uso, "ragionato", del computer consente, anche a un ragazzo di seconda superiore, di trovare le soluzioni di una equazione del tipo  f(x) = k  con f descrivibile mediante le funzioni incorporate nel software (con una precisione sufficiente per tutti gli scopi pratici), con degli zoom o, se la funzione è continua, con il metodo di bisezione;
•  e, eventualmente, accennare agli alunni che solo per alcune classi di equazioni esistono delle formule risolutive (anche per quelle polinomiali, anche se con tecniche di cui gli alunni non dispongono).