Se definisco √2 come il numero il cui quadrato è 2, come spiego agli alunni che un tale numero esiste?
La spiegazione è semplice, se accoppiata al modo in cui calcolare √2. Nei libri di testo invece in genere o si prende implicitamente per buono che esista un numero che al quadrato faccia 2 o lo si spiega con buffe (e quasi sempre errate) costruzioni dei numeri reali a partire dai razionali.
C'è un numero che moltiplicato per sé stesso faccia 2?
Con 1*1 ho 1, con 2*2 ho 4; deve stare tra 1 e 1. Con 1.1*1.1 ho 1.21, …, con 1.4*1.4 ho 1.96, con 1.5*1.5 ho 2.25; deve stare tra 1.4 e 1.5. Con 1.41*1.41 ho 1.9881, con 1.42*1.42 ho 2.0164; deve stare tra 1.41 e 1.42. Con ... 1.414*1.414 ho 1.999396, con 1.415*1.415 ho 2.002225; deve stare tra 1.414 e 1.415. …
Procedendo in modo analogo trovo: 1.4142, 1.41421, 1.414213, 1.4142135, …
Questo è l'unico modo in cui può essere fatto un numero il cui quadrato sia 2.
Il procedimento precedente mi garantisce anche che il quadrato del numero così generato è proprio 2. Infatti il prodotto di due numeri illimitato lo si fa operando sulle sue approssimazioni per difetto e per eccesso, e quanto fatto mi permette di concludere che elevando al quadrato, ossia moltiplicando per sé stesse, le approssimazioni per difetto e per eccesso del numero così trovato a potenze di 10 man mano più piccole ottengo valori che si stringono sempre più attorno a 2.
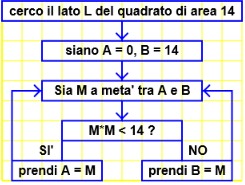
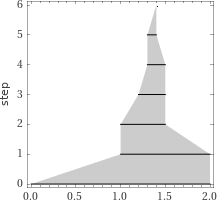
| La spiegazione, opportunamente semplificata, è affrontabile anche nella scuola di base. A rafforzo (o in alternativa) si può usare (riavviandolo più volte) questo script (presente qui). |  |
 |
Qui, negli "esempi", come procedere usando WolframAlpha:
solve x^2 = 2 using bisection method for 0 <= x <= 2 with 1 digits precision |