C'è un numero che moltiplicato per sé stesso faccia 2?  Nei libri di testo si trova che esso viene indicato con √2, e viene chiamato radice quadrata di 2,  ma chi mi garantisce che esista per davvero? Prova ad usare questo programmino e vedi se ti viene qualche idea.

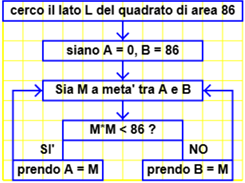
Vediamo che cosa fa il programmino, che cerca il lato di un quadrato che abbia una certa area.  Ogni volta che viene riavviato l'area cambia.  Vediamo quanto accade se l'area è 86.

Prova prendendo la metà di 86, 43, e vede se 43² è maggiore o minore di 86. Se è maggiore restrige la ricerca alla metà a sinistra, tra 0 e 43, se è minore restringe la ricerca alla parte destra, tra 43 e 86.  E così via:

A = 0   B = 86  (A+B)/2 = 43
A = 0   B = 43  (A+B)/2 = 21.5
A = 0   B = 21.5  (A+B)/2 = 10.75
A = 0   B = 10.75  (A+B)/2 = 5.375
A = 5.375   B = 10.75  (A+B)/2 = 8.0625
A = 8.0625   B = 10.75  (A+B)/2 = 9.40625

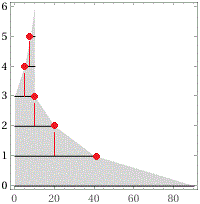
Procedendo in questo modo man mano si restringe, dimezzandosi, l'intervallo in cui cercare il numero, come si vede nella figura sopra a destra.  Andando avanti si ottiene:

...
A = 9.273618495494702   B = 9.273618495514256  (A+B)/2 = 9.27361849550448
...
A = 9.273618495495702   B = 9.273618495495704

A questo punto il programma si ferma.  Se fosse in grado di operare con più cifre restringerebbe man mano l'intervallo in cui cercare un numero che al quadrato faccia 86 arrivando a 9.27361849549570375251641607...
In questo modo posso conoscere √86 con tutte le cifre che voglio.  Ho, quindi, dimostrato che √86 effettivamente esiste.

In modo simile posso dimostrare che √2 esiste, e trovarne, potenzialmente, tutte le cifre.

A = 0   B = 2  (A+B)/2 = 1
A = 1   B = 2  (A+B)/2 = 1.5
A = 1   B = 1.5  (A+B)/2 = 1.25
A = 1.25   B = 1.5  (A+B)/2 = 1.375
A = 1.375   B = 1.5  (A+B)/2 = 1.4375
A = 1.375   B = 1.4375  (A+B)/2 = 1.40625
...
A = 1.414213562373095   B = 1.4142135623730954  (A+B)/2 = 1.4142135623730951
A = 1.414213562373095   B = 1.4142135623730951

Posso ottenere l'approssimazione 1.414213562373095. Il valore più preciso sarebbe 1.41421356237309504880168872420969807856967...

Posso, poi, fare tutto più semplicemente con lo script "radice qua." presente QUI:

 

Per gli insegnanti.  Ci sono pochissimi libri di testo in cui ci sia una qualche plausibile giustificazione dell'esistenza della radice quadrata dei numeri positivi, mentre la spiegazione, come abbiamo visto, sarebbe molto semplice.  In molti libri delle superiori sono presenti buffe spiegazioni clamorosamente sbagliate  (basate su errate costruzioni dei numeri reali a partire dai razionali o su definizioni assiomatiche dei numeri reali erronee, in cui non sono presenti assiomi - come la cosiddetta "completezza euclidea" - che garantiscano effettivamente l'esitenza della radice quadrata di ogni numero reale positivo).