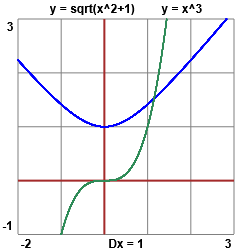
Si vogliono trovare, con una buona precisione, le coordinate del punto in cui si incontrano le due curve rappresentate a fianco, una di equazione y = √(x²+1), l'altra di equazione y = x³. Prova a farlo con un programma in JavaScript, modificando opportunamente il programma considerato nella voce "risoluzione equazioni 1" degli Oggetti Matematici.

Modifico opportunamente il programma, introducendo anche la stampa dell'ordinata del punto di intersezione:

function F(x) {return Math.sqrt(x*x+1)-x*x*x }
a=0; b=2
if(F(a)*F(b)>0) document.write ("F(a) e F(b) hanno segno =")
else {
for(i=0; i<100; i=i+1) {
       m = a+(b-a)/2; y1 = F(a); y2 = F(m); y3 = F(b)
       if(y1*y2 > 0) {a = m} else {b = m} }
    document.write("x = ", m," y = ", m*m*m)
}

Ottengo:   x = 1.150963925257758     y = 1.5247025799298515

La soluzione esatta, non facile da trovare neanche per un laureato in matematica, è
x = √( (9 - √69)^(1/3) + (9 + √69)^(1/3) ) / ( 2^(1/6)·3^(1/3) ) = 1.1509639252577580356...,   y = x³ = ...

Questo esercizio illustra, efficacemente, le potenzialità dell'approccio algortimico alla risoluzione delle equazioni, aspetto, purtoppo, "inspiegabilmente" trascurato dall'insegnamento tradizionale.