Che cosa sono la proprietà del riordino della somma, la proprietà del riordino del prodotto e la proprietà distributiva?

La proprietà del riordino della somma è illustrata dalla seguente immagine:  se cambio l'ordine con cui congiungo tre aste non cambia la lunghezza dell'oggetto che ottengo.

Esempi numerici:

2+3+9 = 5+9 = 14		9+2+3 = 11+3 = 14		3+(9+2) = 3+11 = 14
88 + 250 + 12 + 150 = 88 + 12 + (250 + 150) = 100 + 400 = 500

In generale:  due termini ottenuti entrambi applicando ripetutamente l'addizione a partire dagli stessi sottotermini sono termini equivalenti

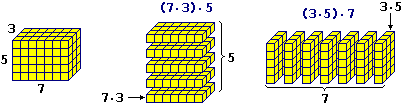
Con ragionamenti fisici ed esperimenti numerici (ad es. osservando che per contare i cubetti della figura seguente posso sia sommare 5 strati di 7·3 cubetti, cioè fare 7·3·5, che sommare 7 strati di 3·5 cubetti, cioè fare 3·5·7) possiamo convincerci che vale anche la proprietà del riordino del prodotto:
due termini ottenuti entrambi applicando ripetutamente la moltiplicazione a partire dagli stessi sottotermini sono termini equivalenti.

Esempio numerico:   25·70·4·3 = 25·4·3·70 = 100·3·70 = 300·70 = 21000

Queste sono proprietà di base, che si apprendono facilmente operando in situazione.  Nei libri di testo della scuola di base invece di queste semplici proprietà vengono introdotte le proprietà associative  [a+(b+c) = (a+b)+c,  a×(b×c) = (a×b)×c]  senza che gli autori si rendano conto che applicando queste proprietà non è affatto facile (non è probabilmente alla loro portata!) dimostrare le equivalenze esemplificate sopra.  L'obiettivo di questi autori è fare imparare a memoria cose da ripetere senza alcun collegamento con le abilità da mettere in atto:  questo, del resto, è lo standard per le definizioni e le dimostrazioni presenti nei libri di testo più diffusi.

Analogamente, interpretando la moltiplicazione come modello matematico per il calcolo dell'estensione di una superficie rettangolare, posso convincermi del fatto che:

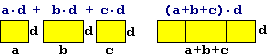
a·d+b·d+c·d  equivale a   (a+b+c)·d  e più in generale del fatto che:
    a(b + c + …) = ab + ac + …   e   (b + c + …)a = ba + ca + …

Questa è la cosiddetta proprietà distributiva della moltiplicazione rispetto alla addizione.

Anche questa proprietà la acquisiamo facilmente (senza formalizzazioni) sin dalle prime eseperienze artitmetiche. Nel fare  5 cento +2 cento = (5+2) cento  usiamo in modo naturale questa proprietà.

          24 x
          32 =
         ————
 24·2 —>  48 +
24·30 —> 720 =
         ————       
         768