Come è noto, esistono tuttora bizzarre proposte didattiche che privilegiano l'introduzione scolastica dei numeri basata sull'approccio cardinale, senza tener conto dell'approccio ordinale e dei molti altri usi del numero con cui il bambino ha a che fare (e su cui ha una relativa padronanza) prima di andare a scuola  [per una breve rassegna apri qui e metti in "trova nella pagina" ordinal per trovare i punti in cui si parla di questo tema; per altri aspetti vedi l'esercizio 26 qui].  Le immagini seguenti richiamano altre considerazioni:

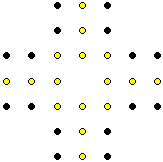
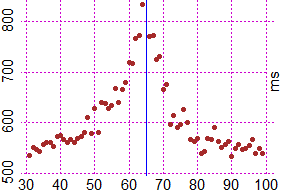
L'immagine a sinistra (relativa a vari esperimenti fatti verso il 1970) illustra un'immagine in cui ci sembra, erroneamente, che i punti "chiari" siano pi numerosi dei punti "scuri".  Quella a destra è un grafico che riporta gli esiti di un esperimento (realizzato verso il 1990, documentato in vari libri ed articoli di scienze cognitive) in cui viene visualizzato il tempo (in ms) che viene impiegato per stabilire se un numero (tra 30 e 100) è maggiore o minore di 65.  Cerca di capire che relazione hanno questi esperimenti con il tema discusso sopra.

    La nostra percezione dei "grandi" numeri di oggetti si basa sulla loro densit e sulla loro disposizione. Nel caso della figura a sinistra il nostro apparato percettivo ci convince, a torto, che i punti chiari siano pi numerosi in quanto appaiono pi concentrati, meno sparsi. Non valutiamo solo la quantit degli oggetti, ma anche il modo in cui occupano lo spazio.
    L'esperimento illustrato dalla figura a destra mette in luce come la nostra valutazione dei numeri obbedisce ad un "effetto misura" (o "effetto distanza"):  ci è pi facile distinguere due numeri lontani tra di loro come 90 e 100 piuttosto che due numeri vicini come 81 e 82 o due numeri come 10 e 20, egualmente distanti ma pi piccoli. Il nostro cervello coglie i numeri nella loro "integralit " e (per noi in modo inconscio) li trasforma in posizioni sulla "linea continua dei numeri": il confronto avviene tra due posizioni, non tra i simboli che rappresentano le quantit .
    Questi ed altri aspetti si possono trovare discussi nel libro di Stanislas Dehaene "La Bosse des maths" (Paris, Odile Jacob, 1997), tradotto in italiano come "Il pallino della matematica" (Mondadori, 2000).

    Per altri aspetti, legati alla nostra percezione spaziale, vedi i paradossi della visione.