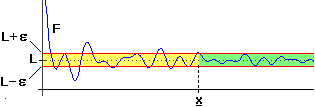
Alla voce limiti abbiamo visto che il fatto che
al crescere di x oltre ogni limitazione (per x → ∞) F(x) tende a stabilizzarsi sul valore L (F(x) → L)
e che abbiamo indicato con la notazione:
lim x → ∞ F(x) = L
può essere precisato nel seguente modo (illustrato dalla figura a lato):
"comunque fissi un numero positivo ε posso trovare un valore x tale che per ogni input x ad esso superiore l'output F(x) disti da L meno di ε".
Precisa in modo simile le condizioni:   limx → kF(x) = L  e  limx → k+F(x) = ∞ (con k numero reale).

lim x → k F(x) = L
Comunque fissi un numero positivo ε posso trovare un altro numero positivo δ tale che per ogni input x diverso e distante meno di δ da k l'output F(x) disti da L meno di ε.
[a lato una descrizione in termini geometrici (è un caso in cui in k si ha una discontinuità)]
limx → k+ F(x) = ∞
Comunque fissi un valore y posso trovare un numero positivo δ tale che per ogni input x maggiore e distante meno di δ da k l'output F(x) sia maggiore di y.
[  Due possibili descrizioni usando simboli logici:  ∀ε > 0  ∃δ > 0  ∀x ∈ (k-δ,0) ∪ (0,k+δ)   F(x) ∈ (L-ε, L+ε)  ∀y  ∃δ > 0  ∀x ∈ (k, k+δ)   F(x) ∈ (y, ∞)   Descrizione simbolica dell'esempio nel testo del quesito:  ∀ε > 0  ∃x  ∀x ∈ (x, ∞)   F(x) ∈ (L-ε, L+ε) ]