| rettangoli | quanti? | 3 | quali? | A, C, D | 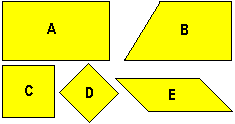 |
| quadrati | quanti? | 2 | quali? | C, D | |
| rombi | quanti? | 2 | quali? | C, D | |
| trapezi | quanti? | 5 | quali? | tutti | |
| parallelogrammi | quanti? | 4 | quali? | A, C, D, E |
Nella seguente illustrazione, quanti e quali sono i rettangoli, i quadrati, i rombi, i trapezi e i parallelogrammi?
rettangoli
quanti? 3
quali? A, C, D

quadrati
quanti? 2
quali? C, D rombi
quanti? 2
quali? C, D trapezi
quanti? 5
quali? tutti parallelogrammi
quanti? 4
quali? A, C, D, E
Di fronte a quesiti di questo genere la grande maggioranza (oltre il 95%) degli alunni sia all'inizio della scuola media che all'inzio delle superiori
considerano rettangolo solo A, pensando erroneamente che i quadrati non siano rettangoli, che invece includono tutti i quadrilateri con gli angoli retti.
Questo errore probabilmente è legato al fatto che, nella vita di tutti i giorni, quando diciamo che un tavolo è rettangolare intendiamo (giustamente)
dire che non è quadrato, altrimenti avremmo detto che è quadrato.
Quando si considera una proprietà all'interno di una definizione o una argomentazione di tipo matematico occorre invece includere anche i casi particolari.
Motivazioni simili sono all'origine di altri difussissimi errori, ad esempio del fatto che molti (oltre il 70%)
considerano come parallelogramma solo E, mentre parallelogrammi sono tutti i quadrilateri che hanno i lati opposti paralleli (quindi lo sono anche i rettangoli),
e che moltissimi (quasi il 100%) escludono dai trapezi (quadrilateri con almeno due lati paralleli) i parallelogrammi.
Molti (circa l'80%) non considerano rombo C, forse perché sono stati abituati a vedere i rombi sempre disposti con le diagonali orizzontali o verticali.
In generale non tengono conto che la disposizione non dovrebbe essere presa in considerazione per stabilire di che figura si tratta
(anche se è vero che a volte si sottintende una certa disposizione, ad es. quando si parla di "base" o di "altezza" di una figura a volte ci
si riferisce non solo alla figura ma anche alla sua disposizione).
La figura seguente riassume le relazioni tra i vari tipi di quadrilateri:
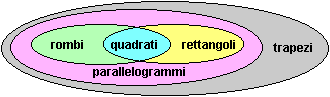
Riassumendo, le difficolt sono legate almeno a due aspetti:
– la tendenza a riferire i diversi tipi di figure a disposizioni standard, che è originata (nel corso degli anni di scuola) da modi stereotipati di raffigurare le figure presenti nei libri di testo e da terminologie scolastiche (come quando di dice che l'area di un rettangolo è "base per altezza" invece che, ad es., "prodotto delle misure di due lati non consecutivi" o che quella di un triangolo è "base per altezza diviso 2" invece che "semiprodotto della misura di un lato per l'altezza ad esso relativa", o, almeno, non si precisa, a parole e con attività opportune, il significato convenzionale dei termini "base" e "altezza");
– la semantica delle frasi del linguaggio comune è diversa da quella usata in matematica per definizioni e descrizioni
di proprietà; legata a questo fenomeno è la difficoltà degli alunni ad accettare come vera la relazione
5 ≤ 9: "5 è minore di 9, perché ingannare dicendo che potrebbe essere uguale a 9?".