Considera le successioni così definite:

x(0) = A, x(n+1) = √x(n) y(0) = 1, y(n+1) = (y(n) + A/y(n)) / 2

Usando una calcolatrice, calcola un po' di elementi delle successioni che si ottengono assegnando ad A i valori seguenti: 4, 2, 100, 0.25. Che cosa puoi congetturare dalle uscite che ottieni?

x) Battendo: 4 [√ ] [√ ] [√ ] ... si può man mano ottenere:
2 - 1.414213562 - 1.189207115 - 1.090507733 - 1.044273782 - 1.021897149 - 1.010889286 - ... - 1.000000661 - 1.00000033 - 1.000000165 - ... - 1.000000006 - 1.000000003 - 1.000000002 - 1.000000001 - 1.000000001 - ...
Battendo: 0.25 [√ ] [√ ] [√ ] ... si può man mano ottenere:
0.5 - 0.7071067812 - 0.8408964153 - ... - 0.9996616065 - 0.9998307889 - ... - 0.9999999994 - 0.9999999997 - 0.9999999999 - 1 - 1 - ...

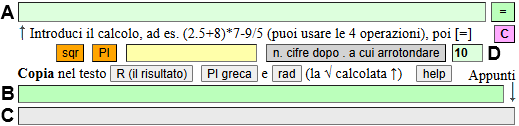
In alternativa posso usare la "piccolissima" calcolatrice presente qui

Batto a destra di [sqr] 4 e poi premendo ripetutamete [sqr] ottengo 2, 1.4142135624, 1.189207115, ..., 1.0000000013, 1.0000000007, 1.0000000004, 1.0000000002, 1. Se invece batto 0.25 ottengo 0.5, 0.7071067812, ..., 0.9999999994, 0.9999999997, 0.9999999999, 1.

La CT si stabilizza in tutti i casi su 1. Possiamo congetturare che, qualunque sia A, positivo, x(.) sia una successione di valori che tende a stabilizzarsi su 1.

y) Nel secono caso posso procedere con una usuale CT o con la stessa calcolatrice online considerata sopra. Consideriamo il caso A = 4.

Metto in C, per ricordarmi che cosa devo calcolare, (R+4/R)/2
Metto (1+4/1)/2 in A, premo [=], ottengo 2.5 in A (e compare (1+4/1)/2 in B); 2.5 è richiamabile premendo [R].
Metto in A (2.5+4/2.5)/2 o, meglio, metto "(", premo [R], metto "+4/", premo [R], metto ")/2" e premo [=]; ottengo 2.05 in A.
Metto in A (usando [R]) (2.05+4/2.05)/2 ottenendo 2.0006097561
Metto in A (usando [R]) (2.0006097561+4/2.0006097561)/2 ottenendo 2.0000000929
Metto in A (usando [R]) (2.0000000929+4/2.0000000929)/2 ottenendo 2
Metto in A (usando [R]) (2+4/2)/2 ottenendo 2 ...

Consideriamo A = 0.25. Metto in C (R+0.25/R)/2
Metto (1+0.25/1)/2 in A, premo [=], ottengo 0.625 in A
Metto in A (usando [R]) (0.625+0.25/0.625)/2 ottenendo 0.5125
Metto in A (usando [R]) (0.5125+0.25/0.5125)/2 ottenendo 0.500152439
Metto in A (usando [R]) (0.500152439+0.25/0.500152439)/2 ottenendo 0.5000000232
Metto in A (usando [R]) (0.5000000232+0.25/0.5000000232)/2 ottenendo 0.5
Metto in A (usando [R]) (0.5+0.25/0.5)/2 ottenendo 0.5 ...

Ovvero, con la "calcolatrice" presente qui mettendo i dati seguenti e premendo ripetutamente [=]:

(2.000000000000002 + 4/2.000000000000002) / 2 = 2
(2.0000000929222947 + 4/2.0000000929222947) / 2 = 2.000000000000002
(2.000609756097561 + 4/2.000609756097561) / 2 = 2.0000000929222947
(2.05 + 4/2.05) / 2 = 2.000609756097561
(2.5 + 4/2.5) / 2 = 2.05
(1 + 4/1) / 2 = 2.5
(B + 4/B) / 2

Analogamente mettendo (B+0.25/B)/2 ottengo:

(0.5000000000000006+0.25/0.5000000000000006)/2 = 0.5
(0.5000000232305737+0.25/0.5000000232305737)/2 = 0.5000000000000006
(0.5001524390243902+0.25/0.5001524390243902)/2 = 0.5000000232305737
(0.5125+0.25/0.5125)/2 = 0.5001524390243902
(0.625+0.25/0.625)/2 = 0.5125
(1+0.25/1)/2 = 0.625
(B+0.25/B)/2

Oltre a: 4 → 2, 0.25 → 0.5 ottengo 100 →10, 2 → 1.414213562373095, … Posso congetturare che, qualunque sia A, positivo, y(.) sia una successione di valori che tende a stabilizzarsi su √A.

I calcoli possono essere eseguiti anche con dei semplici programmini in JavaScript: vedi.

Per altri commenti: successioni neGli Oggetti Matematici.

Considera le successioni così definite:
x(0) = A, x(n+1) = √x(n)	y(0) = 1, y(n+1) = (y(n) + A/y(n)) / 2
Usando una calcolatrice, calcola un po' di elementi delle successioni che si ottengono assegnando ad A i valori seguenti: 4, 2, 100, 0.25. Che cosa puoi congetturare dalle uscite che ottieni?